Can we use the disk method in this integral?

[Amaelle]

Homework Statement:

look at the image

Relevant Equations:

cylindrical coordinates

Goodd day, I have a question regarding an exercice I have already posted

Bvu was very nice and provided this darwing

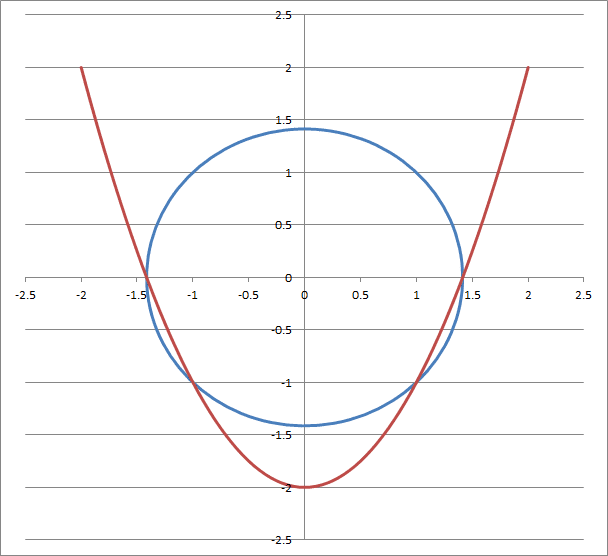
I already have the solution

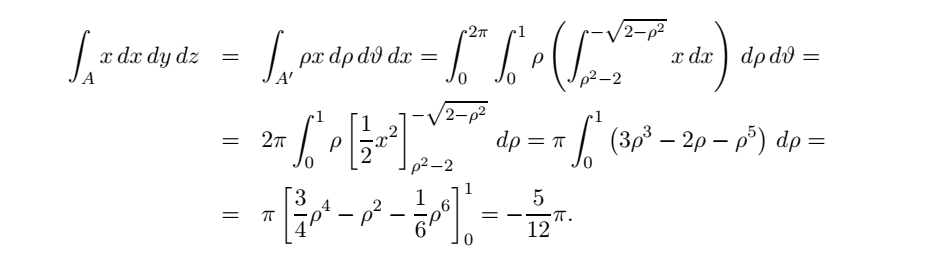But y question is :
can we use the disk method? because as you can see even though the intersection was at x=-1 the sphere goes deep into the paraboloid until x=-sqrt(2)?
so maybe the only way is to caluculate is to

Many thanks in advance!

 

[anuttarasammyak]

$$2\pi\rho d\rho$$ is not disk but ring. So I think your calculation is OK.