- #1
Amaelle
- 310
- 54
- Homework Statement
- integral of int y^2 dxdy over a region (look to the formula inside the exercice)
- Relevant Equations
- y=rcos(theta)
calculate the double integral
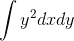
over the region of integration is
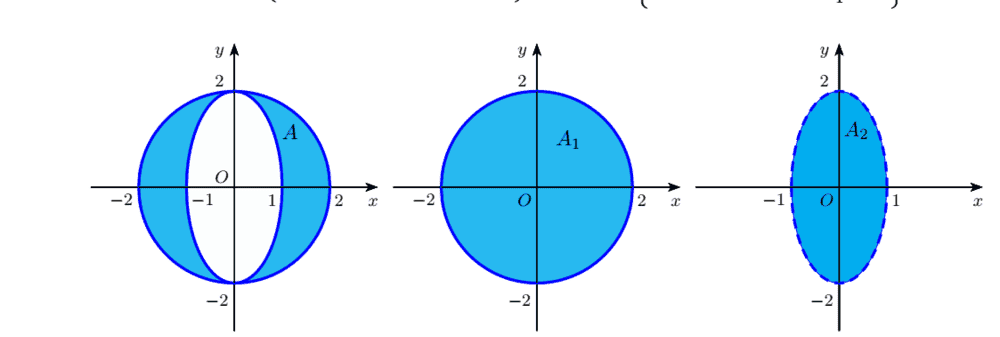
x^2 + y^2 ≤ 4; x^2 + (y/4)^2 ≥ 1
the integrals have been made over two regions
my problem is that when I go to the polar coordinate for the ellipsis and use the jacobian i got 2 instead of 8 ( the following is the professor solution)
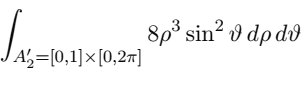
Any help?
many thanks in advance!
over the region of integration is
x^2 + y^2 ≤ 4; x^2 + (y/4)^2 ≥ 1
the integrals have been made over two regions
my problem is that when I go to the polar coordinate for the ellipsis and use the jacobian i got 2 instead of 8 ( the following is the professor solution)
Any help?
many thanks in advance!