SUMMARY
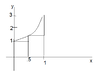
The discussion focuses on evaluating the definite integral of the function \( e^{x^2} \) from 0 to 1, comparing it with the integral of \( e^x \) over the same interval. Participants confirm that \( \int_0^1 e^{x^2}\,dx < \int_0^1 e^x\,dx \), leading to the conclusion that the constant \( a \) defined as \( a = \frac{e-1}{\int_0^1 e^{x^2}\,dx} \) is greater than 1. The conversation emphasizes the need for establishing both upper and lower bounds for the integral of \( e^{x^2} \) to further analyze the value of \( a \).
PREREQUISITES
- Understanding of definite integrals and their properties
- Familiarity with exponential functions, specifically \( e^{x^2} \) and \( e^x \)
- Knowledge of Riemann sums for estimating integrals
- Basic calculus concepts, including comparison of integrals
NEXT STEPS
- Learn techniques for estimating integrals using Riemann sums
- Study the properties of exponential functions in calculus
- Explore the concept of upper and lower bounds for integrals
- Investigate numerical methods for evaluating definite integrals
USEFUL FOR
Students and educators in calculus, mathematicians interested in integral evaluation, and anyone seeking to deepen their understanding of exponential functions and their integrals.