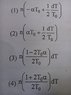SUMMARY
The discussion focuses on calculating the beat frequency produced by a hollow metallic tube closed at one end when subjected to a temperature increase. The relevant equations include the frequency formula for a closed tube, n = v/(4l), and the relationship between frequency, wavelength, and the speed of sound, n = c/λ. Participants emphasize the need to account for the coefficient of thermal expansion (alpha) and the changes in both the speed of sound and the length of the tube due to temperature variations. The challenge lies in expressing the beat frequency in terms of temperature (T) and alpha, while maintaining dimensional consistency.
PREREQUISITES
- Understanding of wave mechanics, specifically sound waves.
- Familiarity with the concept of resonance in closed tubes.
- Knowledge of thermal expansion and its effects on material properties.
- Ability to manipulate equations involving frequency, wavelength, and speed of sound.
NEXT STEPS
- Research the relationship between temperature and the speed of sound in air.
- Study the effects of thermal expansion on the dimensions of materials.
- Learn how to derive beat frequency equations in acoustics.
- Explore the concept of resonance in different types of tubes and their applications.
USEFUL FOR
Students studying physics, particularly those focusing on acoustics and thermodynamics, as well as educators seeking to explain the principles of sound resonance and thermal effects on materials.