Amaelle
- 309
- 54
- Homework Statement
- Convergence of a serie (look at the image)
- Relevant Equations
- absolute convergence, taylor expnasion, asymptotic behaviour!
Good day
here is the exercice
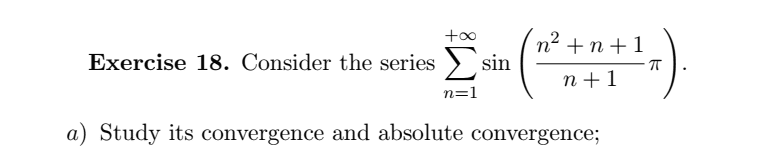
and here is the solution that I understand very well
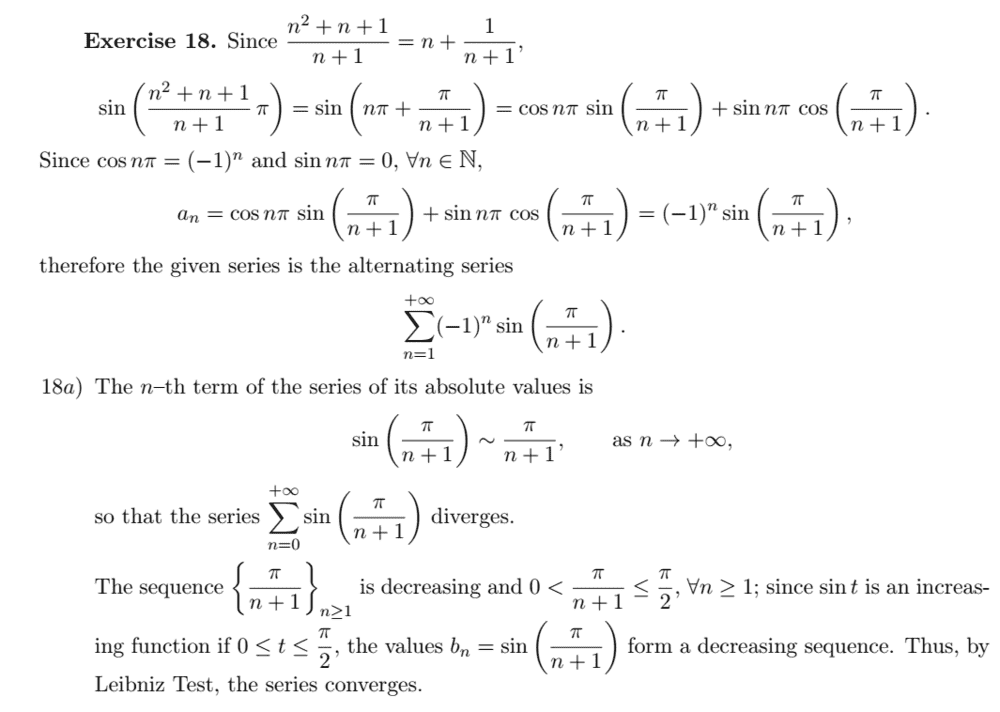
but I have a confusion I hope someone can explain me
if I take the taylor expansion of sin ((n^2+n+1/(n+1))*pi)≈n^2+n+1/(n+1))*pi≈n*pi which diverge!
I know something is wrong in my logic please help me
many thanks in advance!
best regards!
here is the exercice
and here is the solution that I understand very well
but I have a confusion I hope someone can explain me
if I take the taylor expansion of sin ((n^2+n+1/(n+1))*pi)≈n^2+n+1/(n+1))*pi≈n*pi which diverge!
I know something is wrong in my logic please help me
many thanks in advance!
best regards!