Joker93
- 502
- 37
Homework Statement
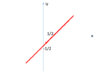
I want to compute ##I=\int_C \dfrac{e^{i \pi z^2}}{sin(\pi z)}##, where C is the path in the attached figure (See below). I want to compute this by converting the integral to one whose integration variable is real.
Homework Equations
There are not more relevant equations.
The Attempt at a Solution
From the path of the integration, we have that ##y=x-\frac{1}{2}##. Thus ##z=x+iy=x(1+i)-\frac{i}{2}##. With this, we can write the integral as
##I=-(1+i)\int_{-\infty}^{+\infty} \dfrac{e^{i \pi (x(1+i)-\frac{i}{2})^2}}{sin(\pi (x(1+i)-\frac{i}{2}))}##.
where we pick up a minus sign due to reversing the direction of integration.
Is this correct? I am using this integral for a more general proof, but it does not seem to fit nicely with the proof. In particular, what makes things ugly is the fact that when we expand the sin function in the denominator of the integrand function, we get things like ##e^{\pm \pi/2}##, which makes me feel not-so-sure about the steps leading from ##z## to ##x##.
Thank you!