Discussion Overview
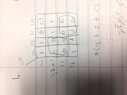
The discussion revolves around the design of a product of sums (POS) circuit for a digital system with four inputs (W, X, Y, Z) and one output (f). Participants are examining the minimization of the equation f(W,X,Y,Z) = M(0,2,4,9,13) + D(6,14) through the use of a truth table, Karnaugh map, and schematic representation using NOR gates. The focus is on verifying the correctness of the minimized equations derived by different participants.
Discussion Character
- Debate/contested
- Technical explanation
- Mathematical reasoning
Main Points Raised
- One participant presents the minimized equation as (y + z + $$\bar{w}$$)($$\bar{z}$$ + w)($$\bar{y}$$ + $$\bar{w}$$).
- Another participant proposes an alternative minimized equation: $(w+z)(\bar{w}+y+\bar{z})$.
- A third participant expresses confusion about how the second participant arrived at their solution, detailing their own grouping method in the Karnaugh map.
- A participant clarifies the notation used in product-of-maxterms, explaining the relationship between minterms and maxterms and the implications for the Karnaugh map.
- One participant confirms their understanding of the function values based on the discussion, indicating a potential correction to their earlier interpretation.
- Another participant suggests that their own minimized equation is still incorrect and proposes a different expression: $$(y + z + w)(y + \bar{z} + \bar{w})(z + w + x)$$.
- Further discussion reveals that while two participants have different expressions, they acknowledge that one is shorter and both are valid up to a "don't care" condition.
- One participant shares a method for using a specific tool to derive the minimal POS from the given function, emphasizing the need to adjust for the tool's grouping method.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the correctness of the minimized equations, as multiple competing views and expressions are presented. The discussion remains unresolved regarding which minimized equation is correct.
Contextual Notes
There are limitations in the understanding of the product-of-maxterms notation and its application in the Karnaugh map, as well as the implications of "don't care" conditions on the validity of different expressions.