Rainbow Cupcake
- 1
- 1
Summary:: prove that (n 0) + (n 1) + (n 2) + ... + (n n) = 2^n is true using mathematical induction.
note that (n n) is a falling factorial
Hello! I have trouble dealing with this problem:
Mod note: Thread moved from math technical section, so is missing the homework template.
Prove that (n 0) + (n 1) + (n 2) + ... + (n n) = 2^n is true using mathematical induction.
note that (n n) is a falling factorial. I have made some progress with this problem but I got eventually got stuck.
progress:
let n=1 (please see attached photo)
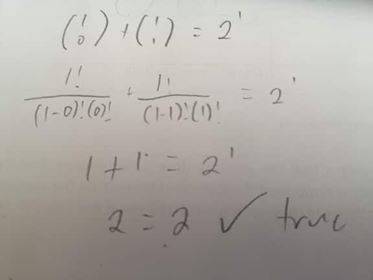
Therefore it is true for n=1
Then we assume that (k 0) + (k 1) + ... + (k k) = 2^k is true. This could also be written as
(k 0) + (k 1) + ... + (k k-1) + (k k) = 2^k.
Prove that (k+1 a) = (k a-1) + (k a) (pls see attached photo for progress)
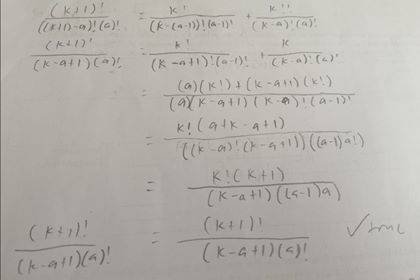
After this step, i got stuck.
Thank you!
note that (n n) is a falling factorial
Hello! I have trouble dealing with this problem:
Mod note: Thread moved from math technical section, so is missing the homework template.
Prove that (n 0) + (n 1) + (n 2) + ... + (n n) = 2^n is true using mathematical induction.
note that (n n) is a falling factorial. I have made some progress with this problem but I got eventually got stuck.
progress:
let n=1 (please see attached photo)
Therefore it is true for n=1
Then we assume that (k 0) + (k 1) + ... + (k k) = 2^k is true. This could also be written as
(k 0) + (k 1) + ... + (k k-1) + (k k) = 2^k.
Prove that (k+1 a) = (k a-1) + (k a) (pls see attached photo for progress)
After this step, i got stuck.
Thank you!
Last edited by a moderator: