Proof that c/a=RootOf(8/3) for Hexigonal Close Packed (HCP)

[colinven]

This is a typical problem in an introductory course to condensed matter physics. I recently solved this problem and had some trouble conceptualizing it, so I thought I would make a post on how to solve the problem.

In general the problem will be stated like this: "Prove that for an ideal HCP \frac{c}{a}=\sqrt{\frac{8}{3}}."

First of all "Ideal" means that the atoms in the basis are solid spheres which are touching one another. Hexigonal close packed HCP looks something like this:

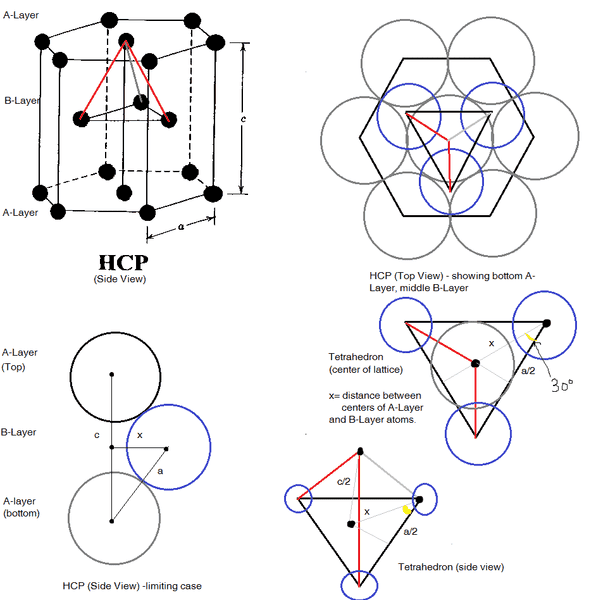. Where 'a' is the distance between the center of the atoms (spheres), and 'c' is the distance between A-Layers (height). The radius of the atoms will be 'a/2' because there are two radii per length 'a'.

The three atoms in the center of the unit cell form a tetrahedron with the base being defined by the three atoms in the B-Layer, and the top vertex is defined by the center atom in the top A-Layer. The height of the tetrahedron is \frac{c}{2} and the length of its base side is 'a'.

In the limiting case: we define 'x' to be the distance between the center of spheres in the A-Layer and B-Layer.

We have two formulas for 'x':

a²-x²=(\frac{c}{2})² (1)

x=\frac{a/2}{cos(30)} =\frac{a}{\sqrt{3}} (2)Next substitute (2) into (1) and after some algebra you should get the result of

\frac{c}{a}=\sqrt{\frac{8}{3}}

 

[annaphys]

I'm not getting how you found the bottom right diagram in the photo. a and are perpendicular to each other. That means the right angle should be between a and c and not between x and c. And then (2) doesn't really make sense. The photos don't really seem consistent.