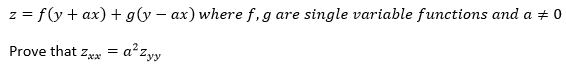Yankel
- 390
- 0
Hello,
I need to do this proof here:
View attachment 2008
I tried but didn't get what I wanted, so I was re-thinking the whole thing.
If I say u=y+ax and v=y-ax, should I do something like (dz/df)*(df/du)*(du/dx)+...?
Because I tried just with u and v (without f and g), and I got almost what I wanted, with a little minus away from proofing, but I think I got it wrong from the start...
I need to do this proof here:
View attachment 2008
I tried but didn't get what I wanted, so I was re-thinking the whole thing.
If I say u=y+ax and v=y-ax, should I do something like (dz/df)*(df/du)*(du/dx)+...?
Because I tried just with u and v (without f and g), and I got almost what I wanted, with a little minus away from proofing, but I think I got it wrong from the start...