fab13
- 300
- 7
I am working on a project which consists in calculating numerically the trajectory of a light ray in the Friedmann-Lemaitre metric with the case "k = 0" (euclidean space) and zero cosmological constant.
The light ray is emitted by a source galaxy at instant ##t_{0}=\dfrac{2}{3H_{0}}## (today) and at a distance taken as a parameter (which I think, is called "comoving distance") and is equal to :$$d_{comoving}=R_{0}\,r_{0}$$
with ##R_{0}## the scale factor of today and ##r_{0}## the radial coordinate.
In my program, I have taken an initial value of ##3000 Mpc## for the physical distance of light ray emitted (##d_{comoving}=3000 Mpc##).
Equations of propagation of this light ray are deduced from the following equations :
$$\dfrac{\text{d}^2 u^{i}}{\text{d}s^2}+\Gamma^{i}_{jk}\,\dfrac{\text{d}u^{j}}{\text{d}s}\,\dfrac{\text{d}u^{k}}{\text{d}s}=0
$$
So, I get finally a differential system that I numerically solve (with ##(t,r,\theta,\phi)## the values of variables to find).
For example, the time equation of this system is :
$$\dfrac{\text{d}^{2}ct}{\text{d}s^{2}} =
-\dfrac{2}{3}\,R_{0}^{2}\,\bigg(\dfrac{3\,H_{0}}{2\,c}\bigg)^{4/3}\,(ct)^{1/3}\,\bigg(\bigg(\dfrac{\text{d}r}{\text{d}s}\bigg)^{2}+r^2\,\bigg(\dfrac{\text{d}\,\theta}{\text{d}s}\bigg)^{2}+r^{2}\,\text{sin}^{2}(\theta)\,\bigg(\dfrac{\text{d}\phi}{\text{d}s}\bigg)^{2}\bigg)$$
by taking for scale factor the following analytical formula :
$$R(t)=R_{0}\bigg(\dfrac{3H_{0}t}{2}\bigg)^{2/3}$$
and with ##s## an affine parameter.
Actually, I have taken ##R_{0}=1## in my code, thinking this would make results easier to handle.
Below on the image, the results that I have got :
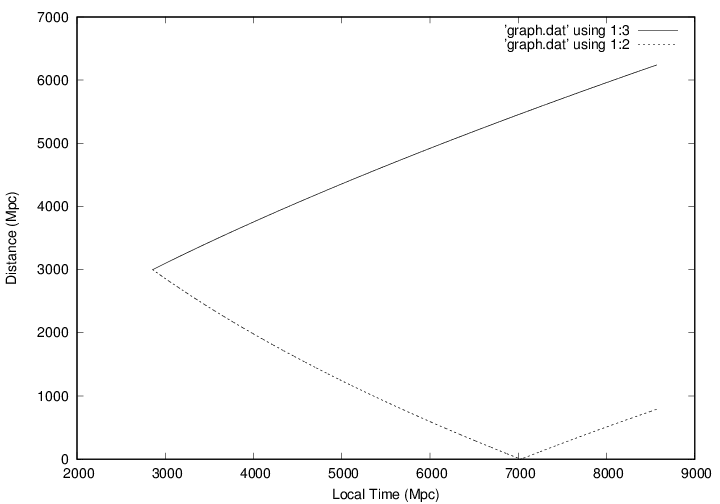
On ##Ox## axis is represented the local time of our galaxy. on ##Oy## the distance betweeen us and the source galaxy emitting.
Solid line represents the trajectory of the source galaxy (which is moving away from us with a distance : $$d_{source}(t)=R(t)r_{0}$$ with ##t>t_{0}##).
Dashed line represents the trajectory of the light ray from source galaxy to our galaxy.
As you can see, light ray reaches our galaxy at a cosmic time about ##7## Giga parsec/c, i.e ##21## Billion years (what is very high, I admit but the problem is not about this). Don't pay attention about the bounce, it is just that I impose a positive value for radial coordinate ##r##.
What I would like to know is if I have to multiply or not the set of all numerical values of radial coordinate (##(r_{i})##) by the scale factor corresponding to time ##t=t_{i}## to get the physical distance of the light ray relatively to our galaxy.
On the above image, I didn't multiply the radial coordinates values ##(r_{i})## by :
$$R(t_{i})/R_{0}=\bigg(\dfrac{3H_{0}t_{i}}{2}\bigg)^{2/3}$$
If I multiply each radial coordinate ##r_{i}## by ##R(t_{i})/R_{0}##, I get the following results :
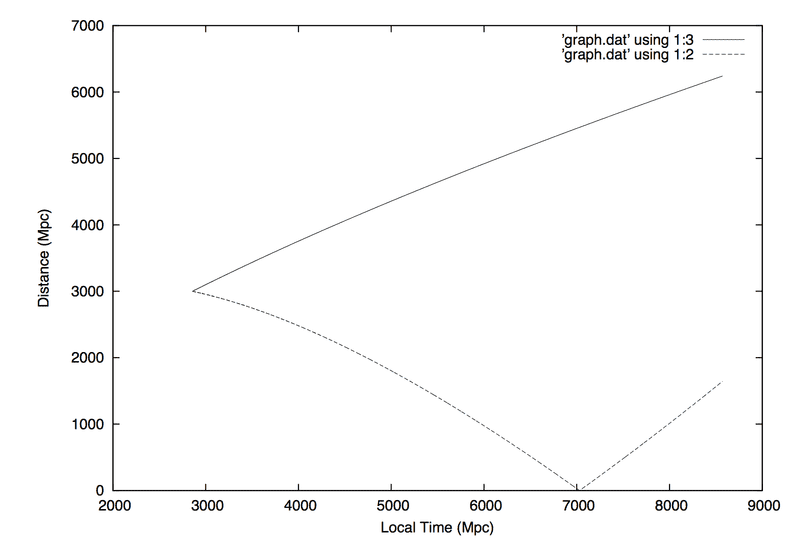
As you can see in comparison with the first image, the form of the trajectory curve is not the same, an in the same time, the convexity is not also the same : on the first results (without multiplying by ##R(t_{i})/R_{0}##), the curve of trajectory is convex whereas with multiplying, the curve of trajectory is concave :
From this difference of convexity between the 2 results, can we make a choice and conclude about the right method to apply, i.e multiply or not by ##R(t_{i})/R_{0}## each numerical value of radial coordinate solved from the differential system ?
Any help or remark is welcome,
Regards
The light ray is emitted by a source galaxy at instant ##t_{0}=\dfrac{2}{3H_{0}}## (today) and at a distance taken as a parameter (which I think, is called "comoving distance") and is equal to :$$d_{comoving}=R_{0}\,r_{0}$$
with ##R_{0}## the scale factor of today and ##r_{0}## the radial coordinate.
In my program, I have taken an initial value of ##3000 Mpc## for the physical distance of light ray emitted (##d_{comoving}=3000 Mpc##).
Equations of propagation of this light ray are deduced from the following equations :
$$\dfrac{\text{d}^2 u^{i}}{\text{d}s^2}+\Gamma^{i}_{jk}\,\dfrac{\text{d}u^{j}}{\text{d}s}\,\dfrac{\text{d}u^{k}}{\text{d}s}=0
$$
So, I get finally a differential system that I numerically solve (with ##(t,r,\theta,\phi)## the values of variables to find).
For example, the time equation of this system is :
$$\dfrac{\text{d}^{2}ct}{\text{d}s^{2}} =
-\dfrac{2}{3}\,R_{0}^{2}\,\bigg(\dfrac{3\,H_{0}}{2\,c}\bigg)^{4/3}\,(ct)^{1/3}\,\bigg(\bigg(\dfrac{\text{d}r}{\text{d}s}\bigg)^{2}+r^2\,\bigg(\dfrac{\text{d}\,\theta}{\text{d}s}\bigg)^{2}+r^{2}\,\text{sin}^{2}(\theta)\,\bigg(\dfrac{\text{d}\phi}{\text{d}s}\bigg)^{2}\bigg)$$
by taking for scale factor the following analytical formula :
$$R(t)=R_{0}\bigg(\dfrac{3H_{0}t}{2}\bigg)^{2/3}$$
and with ##s## an affine parameter.
Actually, I have taken ##R_{0}=1## in my code, thinking this would make results easier to handle.
Below on the image, the results that I have got :
On ##Ox## axis is represented the local time of our galaxy. on ##Oy## the distance betweeen us and the source galaxy emitting.
Solid line represents the trajectory of the source galaxy (which is moving away from us with a distance : $$d_{source}(t)=R(t)r_{0}$$ with ##t>t_{0}##).
Dashed line represents the trajectory of the light ray from source galaxy to our galaxy.
As you can see, light ray reaches our galaxy at a cosmic time about ##7## Giga parsec/c, i.e ##21## Billion years (what is very high, I admit but the problem is not about this). Don't pay attention about the bounce, it is just that I impose a positive value for radial coordinate ##r##.
What I would like to know is if I have to multiply or not the set of all numerical values of radial coordinate (##(r_{i})##) by the scale factor corresponding to time ##t=t_{i}## to get the physical distance of the light ray relatively to our galaxy.
On the above image, I didn't multiply the radial coordinates values ##(r_{i})## by :
$$R(t_{i})/R_{0}=\bigg(\dfrac{3H_{0}t_{i}}{2}\bigg)^{2/3}$$
If I multiply each radial coordinate ##r_{i}## by ##R(t_{i})/R_{0}##, I get the following results :
As you can see in comparison with the first image, the form of the trajectory curve is not the same, an in the same time, the convexity is not also the same : on the first results (without multiplying by ##R(t_{i})/R_{0}##), the curve of trajectory is convex whereas with multiplying, the curve of trajectory is concave :
From this difference of convexity between the 2 results, can we make a choice and conclude about the right method to apply, i.e multiply or not by ##R(t_{i})/R_{0}## each numerical value of radial coordinate solved from the differential system ?
Any help or remark is welcome,
Regards
Last edited: