Prove Homothetic Triangles Concurrent: Ceva's Theorem

[subhradeep mahata]

Homework Statement

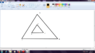
Consider the two homothetic non congruent triangles, with their corresponding sides parallel to each other.
Prove that extended CE, extended DA and extended BF are concurrent.

Homework Equations

The Attempt at a Solution

I can easily solve this using Desargues' theorem. The three points of intersection of corresponding sides are lying on a line, namely the line at infinity. Therefore the three lines connecting corresponding vertices meet in a point. But the task is to prove it using Ceva's theorem, if possible.
I thought of extending CE, DA and BF to touch the opposite sides, but got no clue. Please help me out.

 

[Prof B]

Ignore BF for now. Say that CE and AD intersect at O. By definition, the lines AO, BO, and CO are concurrent. Apply Ceva's theorem to ABC to get a statement about three ratios. Apply Ceva's theorem to DFE get a statement about three other ratios. Use similarity to conclude that two pairs ratios are equal. Use algebra to conclude that the other two ratios are equal. Conclude that another pair of triangles are similar. Conclude that two angles are equal. Conclude that three points are colinear.