Isosceles Triangles with Congruent Lateral Sides

[Born]

Homework Statement

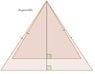
Problem 99 from "Kiselev's Geometry Book I - Planimetry":

Two isosceles triangles with a common vertex and congruent lateral sides cannot fit one inside the other.

Homework Equations

The Attempt at a Solution

The statement is obviously true. If we visualize each isosceles triangle as made from two right triangles then we see that in order for one to fit in the other both the base and the height of one should be smaller than the bade and height of the other, however this is not possible since the sides of the smaller right triangle would not be able to connect to the endpoints of the hypotenuse by the Pythagorean theorem.

Sadly, the Pythagorean theorem comes later in the book. All I have are some more simple theorems, such as "the greater angle opposes the greater side" and "the greatest slant drawn from a point to a line is the one with the greatest distance from the foot of the perpendicular of the line to the point".

Any help is welcome

 

[Cake]

So I take i this is a true or false question?

If so, I'm not sure what the question means by "fit inside." If it means one has to be smaller than the other than I think you're right. If "fit inside" means their vertices and sides line up, I think you have an issue with your answer since the triangles are also congruent.

 

[Born]

I just uploaded a picture to make it clearer.

 

[RUber]

Right. If you decrease the vertex angle but keep the leg length the same, you should be able to use the "greater angle opposes the greater side" property you mentioned to show the new triangle would pop out the bottom of the original.

 

[Born]

Yes, that makes sense. However, what I want to pove is that if the base and height of a right triangle are inside another then the hypotenuses cannot be congruent. If I can prove that then the isosceles triangles can be argumented to be case of two pairs of juxtaposed right triangles

 

[RUber]

@Born, it sounds like you are still trying to use the logic based on the Pythagorean theorem. You are given the fact that your hypotenuses are congruent. Based on the theorems you listed in post 1, your best argument would be based upon angle measure.
Using the juxtaposed right triangle line of thinking, you should be able to list out the possible cases: 1) increase top angle, 2) decrease top angle -- Since the vertex and lateral sides are congruent, you only have a short argument for both cases to say that neither cases can fit inside the original. Only the congruent triangle would fit on the original.