- #1
Richie Smash
- 293
- 15
Homework Statement
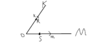
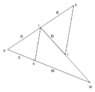
Hi I have attached an image which shows OK and OM which are position vectors such that OK=k and OM =m
R is the mid point of OK and S is a point on OM such that (vec) OS = 1/3 OM
L is the midpoint of RM, using a vector method, prove RS is parallel to KL.
Homework Equations
The Attempt at a Solution
SO the questions asked me to find these vectors
MK=k-m
RM= m-k/2
KS= m/3-K
RS= m/3-k/2
So now tht I've found these vectors,
I would think that I need to prove that KL and RS are multiples of one another to show they are parallel.
First I found the coordinates of L which is the midpoint of RM
L= (m-k/2)/2= m/2-k/4
So now that I know L... I find KL which would be : -k+(m/2-k)=m/2-2k
SO I know KL, and I know RS which is : m/3-k/2
But they don't seem to be multiples of each other... can anyone help me?
Attachments
Last edited: