Pulley and Mass: How to Calculate Velocity?

[the_dialogue]

Homework Statement

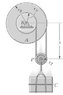
See attached image.

I'm wondering how one would express the velocity of C with respect to the angular velocity of the pulleys and the radii.

Homework Equations

v=w*r

The Attempt at a Solution

I've never quite done double pulleys such as these. Usually, If i had a single object attached, using one cable, to the edge of a pulley, its velocity would be 'v=wr' where 'r' is the radii of the pulley where the cable lies. But how about this case?

PS. This is not an assignment. It's merely a question I came across reading my book.

 

[Doc Al]

Hint: As the double pulley turns, the cable unwinds from each pulley at the same speed as the tangential speed of the rim. Hint2: If the cable is lengthens by a amount L, how far does the lower pulley drop?

 

[the_dialogue]

Tell me if this is right:
If the right cable unwinds at v=w*r_b and the left cable at v=w*r_a, then c moves at v = w*r_b - w*r_a

 

[Doc Al]

Tell me if this is right:
If the right cable unwinds at v=w*r_b and the left cable at v=w*r_a, then c moves at v = w*r_b - w*r_a

What if r_a = r_b? Would your answer make sense then?

 

[the_dialogue]

Indeed it would not.

In that case I'm stuck!

 

[the_dialogue]

Anyone?
------

 

[vanesch]

Tell me if this is right:
If the right cable unwinds at v=w*r_b and the left cable at v=w*r_a, then c moves at v = w*r_b - w*r_a

I think you should consider that v is a linear function of r_a and r_b, so v = u1.r_a + u2.r_b. Now, consider first r_a = 0 which allows you to determine the coefficient u2. Next, put r_b = 0, which allows you to find u1. This should give you the overall expression ; check it for a specific case...

 

[Doc Al]

I recommend that you play around with a piece of string until you figure it out. If you don't have a pulley handy, wrap the string around a tin can and unwind it. This will help you visual what's going on and figure out how the lengthening of the string relates to the turning of the pulley. Treat the double pulley as two single pulleys of different radii (since that's what they are!).

You can also use this method to figure out how the position of C depends on the length of hanging chain. If the string lengthens by 4 inches, how far does C fall?

Review the hints I gave in post #2.