- #1
jeffrey
- 13
- 2
- Homework Statement
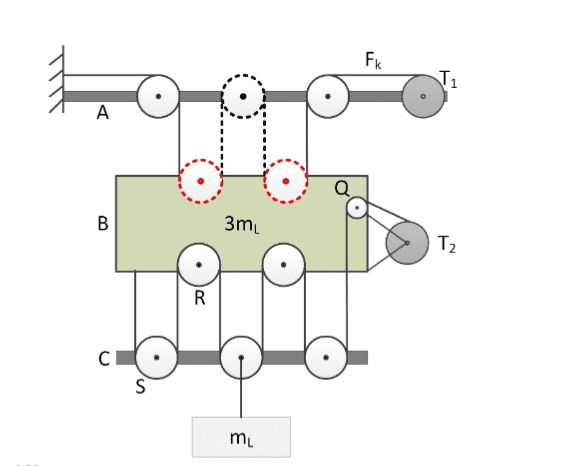
- Suppose mass mL has a constant vertical speed v while hoisting, block B is stationary. In that case, calculate the rotational speeds ωQ, ωR and ωS of discs Q, R and S expressed in v and D. Define clockwise as positive
- Relevant Equations
- v=omega*radius
length_a+length_b= constant
Further given:
- every beam is infinite stiff
- pulleys are massless
- cables don't stretch, no slip, and frictionless.
-Every pulley has a diameter D except pulley Q. Pulley Q has diameter 0.5*D
So what I don't understand is how to calculate/determine the velocity at R and S. Can someone help me or send me into the right direction? I know from the answers that the velocity at R is 2v and at C is 1v, but I don't understand why.
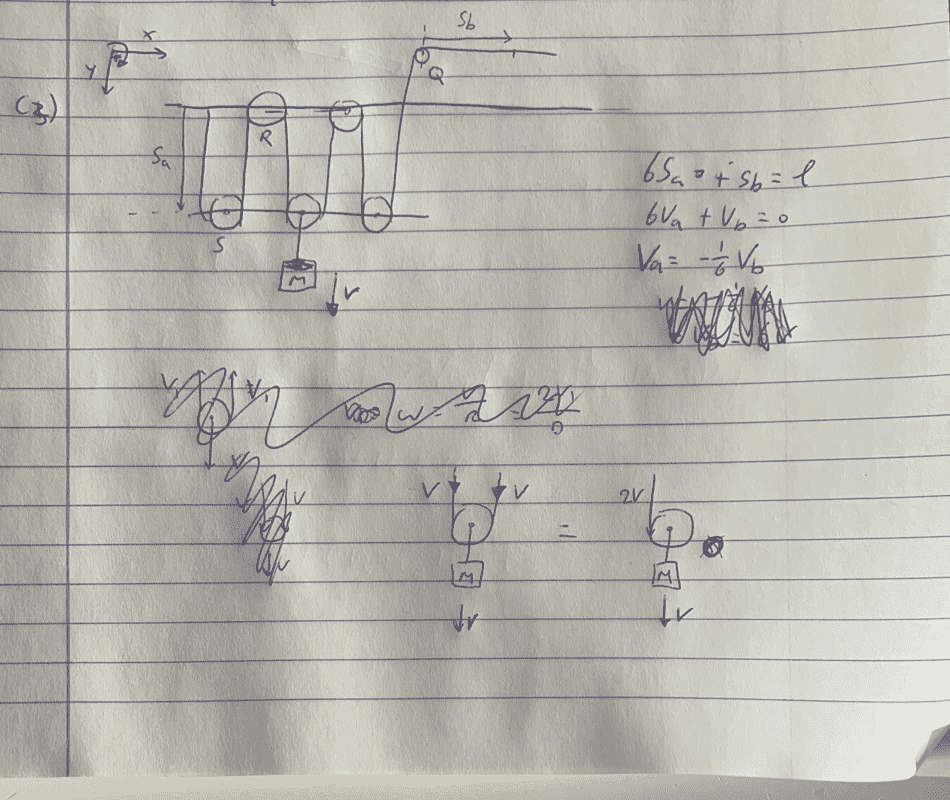
- every beam is infinite stiff
- pulleys are massless
- cables don't stretch, no slip, and frictionless.
-Every pulley has a diameter D except pulley Q. Pulley Q has diameter 0.5*D
So what I don't understand is how to calculate/determine the velocity at R and S. Can someone help me or send me into the right direction? I know from the answers that the velocity at R is 2v and at C is 1v, but I don't understand why.