Pulley at an Angle Problem - Newton Forces

[Lori]

Homework Statement

Homework Equations

Friction Force = normal force * static coefficient for friction
Fnet = ma

The Attempt at a Solution

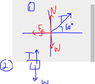
So i drew the free-body diagrams for both the objects...[/B]
Im trying to figure out the tension in the 2nd free body diagram and i know that it's equal to the weight of the object (which i want)...

I was wondering which tension in the first body diagram equals the tension to the 2nd object? I found that Friction = 684 (1520*0.45) thus the component force in the x direction for the rope should be 684.

I then found the hypotenuse of that to find Tension, which is Tcos(60) = 684 and found that T = 1184... but it's not really that close to the answers in the problem! (it is closest to 1898 N, but I am not sure if that's the correct answer)

What did i do wrong!?

 

[kuruman]

Can you show the equation that you used to get the normal force and from it the maximum force of static friction?

 

[RedDelicious]

I'm not sure what it is you're doing. Why are you trying to find tension? As you said, the tension is the weight of the hanging block, so you already the know tension. The problem is to then find the maximum weight of the hanging block (i.e., maximum tension) for which the system is stationary.

Under what condition will the first block begin to move in the x direction?

 

[Lori]

I'm not sure what it is you're doing. Why are you trying to find tension? As you said, the tension is the weight of the hanging block, so you already the know tension. The problem is to then find the maximum weight of the hanging block (i.e., maximum tension) for which the system is stationary.

Under what condition will the first block begin to move in the x direction?

Wait I'm confused. I don't know tension cause I don't know the weight of the hanging block?

 

[kuruman]

You don't know what it is but you know it is equal to the hanging weight because everything is at equilibrium. The hanging weight is what you are looking for, so call it W and proceed with the calculation. In the end you should be able to find a value for W.

 

[haruspex]

Wait I'm confused. I don't know tension cause I don't know the weight of the hanging block?

RedDelicious' post is rather confusing. Not sure what was intended. Ignore that and try to answer Kuruman's question in post #2.

was wondering which tension in the first body diagram equals the tension to the 2nd object?

There is only one tension in each diagram. Can you think of a reason why they should or should not be equal?

 

[Lori]

RedDelicious' post is rather confusing. Not sure what was intended. Ignore that and try to answer Kuruman's question in post #2.

There is only one tension in each diagram. Can you think of a reason why they should or should not be equal?

Hold on, I'll work on this problem later, but to answer your question , I suppose the rope that connect the objects must have the same tension

 

[haruspex]

the rope that connect the objects must have the same tension

Yes, but it is interesting to prove it. Consider the torque balance on the pulley.

 

[Lori]

RedDelicious' post is rather confusing. Not sure what was intended. Ignore that and try to answer Kuruman's question in post #2.

There is only one tension in each diagram. Can you think of a reason why they should or should not be equal?

I'm trying to solve for W , but i keep getting that T = 1368 = W??

I did this since Friction force would be 684 so that means that x components must balance out for the x forces. Thus, i did the 684/cos(60) to find the tension of the rope which i know equals the weight of the hanging mass??

 

[haruspex]

since Friction force would be 684

That is why you need to respond to kuruman's post #2. Write out the equations by which you deduce that.

 

[Lori]

That is why you need to respond to kuruman's post #2. Write out the equations by which you deduce that.

Friction = 0.4N

N = cos60 = ?/T

N + T = 1520

Friction = 0.4 (1520-T)

 

[haruspex]

Friction = 0.4N

Yes.

N = cos60 = ?/T

I don't understand what you mean by that.

N + T = 1520

The tension is not vertical.

 

[Lori]

Yes.

I don't understand what you mean by that.

The tension is not vertical.

Is normal force not going to be equal to the weight of the object because tension is involved? So that the tension's y component + the normal force = 1520 ( weight of object)

 

[Abhishek kumar]

Here is solution hope u understand and T=weight of hanging block

 

[haruspex]

Is normal force not going to be equal to the weight of the object because tension is involved? So that the tension's y component + the normal force = 1520 ( weight of object)

Right.

 

[haruspex]

Here is solution hope u understand and T=weight of hanging block

This is a homework forum. The rule is to post hints, point out errors, etc. Please do not post complete solutions.

 

[Lori]

Ahhh. Thank you. I understand what you guys were wanting me to do... I think the problem was that I plugged in numbers to early on, and I should have written the equations that showed equilibrium in the x and y directions. .

Thanks everyone [emoji32]

Slowly understanding physics!

 

[Abhishek kumar]

Ok

This is a homework forum. The rule is to post hints, point out errors, etc. Please do not post complete solutions.

Ok from now onwards i will keep in mind that