Pulley problem with moment of inetia

Click For Summary

Homework Help Overview

The problem involves a system with two blocks connected by a cord over a pulley, where one block is affected by friction. The pulley has mass and a moment of inertia, which complicates the calculation of acceleration for the blocks. Participants are exploring the dynamics of the system, particularly how the moment of inertia of the pulley influences the overall motion.

Discussion Character

  • Mixed

Approaches and Questions Raised

  • Participants discuss the use of free body diagrams to analyze the forces acting on the blocks and the pulley. There are questions about how to incorporate the moment of inertia into the equations of motion, particularly in relation to the angular acceleration of the pulley and its effect on the linear acceleration of the blocks.

Discussion Status

The discussion is ongoing, with participants raising questions about the role of the moment of inertia in the problem. Some have expressed uncertainty about how to start the analysis, while others are attempting to clarify the relationship between linear and angular acceleration in the context of the pulley system.

Contextual Notes

Participants are working under the assumption that the cord does not slip over the pulley and that the mass of the cord is negligible. There is a focus on understanding the implications of the pulley having mass and friction, which is different from simpler problems where the pulley is considered massless.

Iansno1
Messages
2
Reaction score
0
Problem

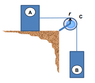
As shown below, Block A has mass 'M' and rests on a surface with a coefficient of kinetic friction 'Uk' .The cord attached to A passes over a pulley at C and is attached to a block B of mass '2M'. If B is released calculate the acceleration of A.

Assume the cord does not slip over the pulley. The Pulley can be approximated as a thin disk of radius 'r' and mass 'M/4' . Neglect the mass of the cord
Relevant equations

moment of inertia of the disk: I=0.5*M*r2
Not sure where to start
 

Attachments

  • Capture.PNG
    Capture.PNG
    4.7 KB · Views: 449
Physics news on Phys.org
with free body diagrams?

ehild
 
How does the Moment of inertia come into the equation? I can do these problems when the pulley is assumed to have no mass and no friction.
 
Iansno1 said:
How does the Moment of inertia come into the equation? I can do these problems when the pulley is assumed to have no mass and no friction.

Moment of inertia is the analog of mass for rotational motion. The moment of inertia resists angular acceleration in the same fashion as mass resists linear acceleration.

In this problem the pulley adds resistance to the acceleration of the overall system because the cord does not slip, and so must cause angular acceleration of the pulley. The angular acceleration is related to the linear acceleration (how?).
 

Similar threads

Mass and pulley system (Rotational Dynamics)
  • · Replies 9 ·
Replies
9
Views
2K
Ideal Vs Real Mass Pulley system
  • · Replies 10 ·
Replies
10
Views
5K
How Do You Calculate the Angular Motion of a Pulley System?
  • · Replies 15 ·
Replies
15
Views
2K
Moment of Inertia with pulley and two masses on a string (iWTSE.org)
  • · Replies 8 ·
Replies
8
Views
15K
Newton's Second Law (Pulley Sustem)
  • · Replies 3 ·
Replies
3
Views
2K
Pulley's mass is invariant to the physics problem?
  • · Replies 13 ·
Replies
13
Views
1K
Problem with pulleys - two fixed and one movable
  • · Replies 22 ·
Replies
22
Views
2K
Friction problem involving a pulley
  • · Replies 10 ·
Replies
10
Views
3K
Experimental Design: Pulley and Mass Hangers
  • · Replies 30 ·
2
Replies
30
Views
4K
System of two pulleys and three masses
  • · Replies 22 ·
Replies
22
Views
7K