khkwang
- 57
- 0
Not exactly a homework question, but I need to know this before I can answer the question
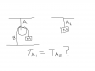
There's a pulley suspended from a rope A. Hanging from the pulley from one side is a mass m. "Hanging" off the other side of a pulley is simply the same rope (which is attached to the mass) (rope B), attached to the ground.
Is the tension on rope A simply mg?
none
I know the tension on rope B would be mg. But I'm wondering about rope A. I don't know whether to count the side of rope B attached to the ground as a contributing factor in the tension of rope A.
The way I see it is that since rope B is attached to the ground, the only thing that moves if one were to pull on rope A would be mass m. Thus the only work done is on mass m, and the only force required to move mass m would be needed: mg.
So then the tension on both ropes would be mg?
Homework Statement
There's a pulley suspended from a rope A. Hanging from the pulley from one side is a mass m. "Hanging" off the other side of a pulley is simply the same rope (which is attached to the mass) (rope B), attached to the ground.
Is the tension on rope A simply mg?
Homework Equations
none
The Attempt at a Solution
I know the tension on rope B would be mg. But I'm wondering about rope A. I don't know whether to count the side of rope B attached to the ground as a contributing factor in the tension of rope A.
The way I see it is that since rope B is attached to the ground, the only thing that moves if one were to pull on rope A would be mass m. Thus the only work done is on mass m, and the only force required to move mass m would be needed: mg.
So then the tension on both ropes would be mg?