Pump work required to reach a maximum reservoir height

[lonewolfx]

Homework Statement

Consider the represented system, where a water (density 1000kg/m³, dynamic viscosity 0.001kg/(m.s)) flows at a rate of 500 L/min in a smooth PVC duct with 5 cm of internal diameter. The suction duct is immersed 0.5 m into the water, and the remaining dimensions are indicated in the figure. The 90º elbows are of threaded type (K = 1.5). For this situation, as height "d" increases, the water flow rate discharged in the upper reservoir decreases. There is a maximum height "d" for which flow rate is null. Knowing that the pump efficiency is 90%, find the height "d" that guarantees a null flow of water in the discharge of the upper reservoir, and find the power required to drive the pump under such conditions.

Relevant Equations

General energy conservation equation for an incompressible fluid, and neglecting changes in internal energy:
$$ \frac{P_1}{(\rho g)} + z_1 + \frac{v_1^2}{2g} - H_F + H_P = \frac{P_2}{(\rho g)} + z_2 + \frac{v_2^2}{2g} $$
Where $v$ is the fluid's velocity, $g$ is the local acceleration due to gravity (consider 9.81 m/s²), $P$ is the pressure, $H_P$ is the pump's manometric height, $H_F$ represents continuous and local losses, $z$ is the relative height of the fluid, $\rho$ is the fluid's density.
Continuous losses along the tube can be computed using the equation:
$$(H_F)_{cont} = f \frac{L}{D} \frac{v^2}{2g} $$
Where $f$ is the friction facto, $L$ is the total length of the tube, $D$ is the tube's diameter.
Local losses equation:
$$ (H_F)_{local} = K \frac{v^2}{2g} $$
Pump efficiency:
$$\eta = \frac{\dot{W}_{P}}{\dot{W}_{total}} $$
$\dot{W}_{P}$ is the work done by the pump on the fluid, $\dot{W}_{total}$ is the total work provided to the pump.
$$ \dot{W}_P = H_P \rho g \dot{V} $$
Where $\dot{V}$ is the volumetric flow rate.
Fluid velocity:
$$ v = \frac{\dot{V}}{(\pi D^2/4)} $$
$D$ is the diameter of the tube.

The following image represents the system under analysis:

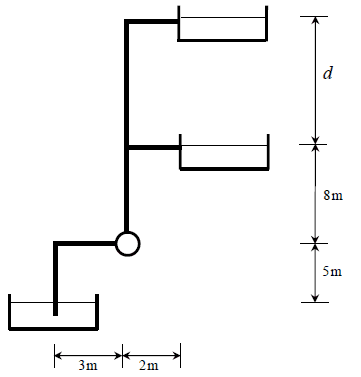
Using a reference point 1 on the surface of the lower reservoir, point 2 at the discharge of the middle reservoir, and point 3 at the discharge of the upper reservoir, and assuming the pressure is equal to atmospheric pressure at all of these points, the energy conservation equation, under steady state conditions will take the following form:
$$ z_1 + \frac{v_1^2}{2g} - (H_F)_1 - (H_F)_2 - (H_F)_3 + H_P = z_2 + \frac{v_2^2}{2g} + z_3 + \frac{v_3^2}{2g} $$
where $z_1 = 0$, $z_2 = 13\ m$, $z_3 = 13+d\ m$. According to the problem statement, the volumetric flow rate at 3 is zero, so $v_3 = 0$, and therefore $(H_F)_3 = 0$ as well since all of the equations involve a velocity squared term. The velocity at point 1 (surface of the lower reservoir) is approximately zero if we assume the reservoir to be much greater in diameter than the pipe. This leaves us with $v_2 = \dot{V}/(\pi (D/2)^2) = 4.244\ m/s$ since the flow rate through the first conduit is equal to the flow rate through the second one.
$$ - (H_F)_1 - (H_F)_2 + H_P = 26 + d + \frac{v_2^2}{2g} $$
Reynold's number is equal to 2.122E5; since the flow is turbulent, I used Moody's diagram to read the value of the friction factor. The problem states the pipe is completely smooth, so I used the smooth pipe curve in the diagram. The value I read was 0.0173. Because I assumed the flow rate through the conduit before the pipe and after the pipe to be the same (since the flow rate is null in the third conduit), the velocities in these conduits are also equal to one another (4.244 m/s). The total head loss due to friction is:
$$ H_F = \frac{v^2}{2g} \left( f \frac{L}{D} + K_{elbow} \cdot 2 \right) = \frac{4.244^2}{2\cdot 9.81} \left( 0.0173 \cdot (5+3+8+2)/(0.05) + 3 \right) = 8.471\ m $$
The problem now is that I no longer can continue my solution, as there are more unknowns - the pump's head and height d - than the number of equations. Any help is appreciated, as I have never seen a problem like this one, and I am unsure if the approximations I performed were even correct.

 

[Chestermiller]

The fluid in d is going to be hydrostatic. To determine d, you can calculate the head at the junction between the horizontal tube to the middle reservoir and the vertical tube d. You know the flow rate through this horizontal tube, and you know the outlet pressure. The only ambiguity is how to handle the local loss at the junction.

Meanwhile, none of the flow goes into the d tube, so d doesn't even come into play in calculation of the pump head.

 

[Lnewqban]

Height of column d is proportional to the static pressure at the tee, where you also have dynamic pressure.
That static pressure depends on the restriction to the flow in the 2-meter last section of pipe discharging into the middle tank (at atmospheric pressure).

Please, see:
https://www.engineeringtoolbox.com/pumps-t_34.html