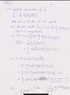SUMMARY
The discussion focuses on calculating trace and purity in quantum mechanics, specifically using the equations Tr(B) = Σ and purity = Tr(ρ^2). The user expresses confusion regarding the application of these concepts in their homework questions. A response clarifies that for question 1, the user needs to specify the state |x_k⟩, and for question 2, they should approach the problem step by step, either by substituting the density operator into its bracket representation or vice versa.
PREREQUISITES
- Understanding of quantum mechanics concepts, particularly density operators
- Familiarity with the mathematical operation of taking the trace
- Knowledge of quantum state notation, including bra-ket notation
- Basic grasp of purity as a measure of quantum state mixedness
NEXT STEPS
- Study the properties of density operators in quantum mechanics
- Learn how to compute the trace of an operator in quantum systems
- Explore the concept of quantum state purity and its implications
- Practice problems involving bra-ket notation and density matrices
USEFUL FOR
Students of quantum mechanics, physicists working with quantum states, and anyone seeking to deepen their understanding of trace and purity calculations in quantum systems.