[QM] Two-Particle Systems: overlapping/non-overlapping wavefunctions

[WeiShan Ng]

Homework Statement

Hi, I was reading Griffiths and stumble upon some questions. This is from 5.1.2 Exchange Forces. The section is trying to work out the square of the separation distance between two particles, $$\langle (x_1 - x_2)^2 \rangle = \langle x_1^2 \rangle + \langle x_2^2 \rangle - 2 \langle x_1 x_2 \rangle$$
My confusion came when
$$\int x_1 \psi_a (x_1)^* \psi_b (x_1) dx_1 \, \int x_2 \psi_b(x_2)^* \psi_a(x_2) dx_2 = \langle x \rangle _{ab} \langle x \rangle _{ba}$$ I don't get why there are $\langle x \rangle _{ab}$ and $\langle x \rangle _{ba}$ here , won't the $$\int x_2 \psi_b(x_2)^* \psi_a(x_2) dx_2=\int x_1 \psi_a (x_1)^* \psi_b (x_1) dx_1=0??$$ since both $\psi_a$ and $\psi_b$ are orthogonal to each other?

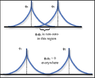
And in the next paragraph the text says

Notice that $\langle x \rangle _{ab}$ vanishes unless the two wavefunctions actually overlap [if $\psi_a(x)$ is zero wherever $\psi_b(x)$ is nonzero, the integral in Equation 5.20 is zero] So if $\psi_a$ represents an electron in an atom in Chicago, and $\psi_b$ represents an electron in an atom in Seattle, it's not going to make any difference whether you antisymmetrize the wave function or not. As a practical matter, therefore, it's okay to pretend that electrons with nonoverlapping wave functions are distinguishable.

What is the meaning of "overlap" here? Based on the text given I assume it means both particles are "at the same position", i.e. $x_1=x_2$. And how does an overlapping and non-overlapping wavefunction look like?

Homework Equations

The Attempt at a Solution

 

[Nguyen Son]

This picture may answer your question "how does an overlapping and non-overlapping wavefunction look like?"

 

[WeiShan Ng]

This picture may answer your question "how does an overlapping and non-overlapping wavefunction look like?"

Thank you!