Quantum erase explained with waves

[DParlevliet]

Someone attended me on the article `A double-slit quantum eraser' from Walborn e.a. 2008. This is a much better, clearer and more detailed described quantum eraser then Kim e.a. A basic explanation is in http://grad.physics.sunysb.edu/~amarch/ . A simplified diagram:

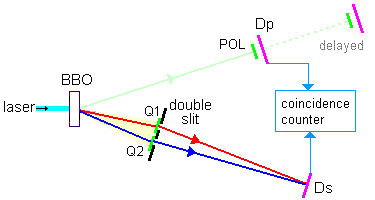
A BBO is radiated with a laser. Now and then the BBO emits two entangled photons. The yellow photon goes through a double slit to signal detector Ds, with a quarter wave plate Q1 or Q2 in each path. They are rotated 90° to each other, so produce a polarization which rotates in opposite directions, depending on the polarization of the incoming photon. The green photon goes to detector Dp, with a polarizing cube POL in the path. Only photons in Ds are registered which coincidence with photons in Dp. Dp is situated closer to the BBO then Ds. So photons are first detected by Dp. The intensity of the beam is so low, that photons are detected before a new photon is emitted by the BBO. So it works with single photons. The results were:
1 Without Q1/2 and POL there was an interference pattern in Ds
2 With Q1/2 there was no interference.
3 With Q1/2 and POL, adjusted on Q1 fast axis, there was interference.
4 With Q1/2 and POL, adjusted on Q2 fast axis, there was interference (but 180º shifted with 3).
5 1-4 with Dp on a larger distance then Ds (delayed eraser), gives the same result.

The article explains this with QM math, and:
2: Q1/Q2 marks the red/blue beams, so one can detect which path the photon went, also when this measurement is not actually done (in 2). This removes the interference pattern.
3-4: When placing POL at a suitable angle, the polarization information is erased, so it is not possible anymore to know which path the photon went. Therefore the interference pattern is back again.

Another way to analyse this measurement is with the classical wave property of the photon, which should give the same result. But it doesn't:

2a The idea is that if the particle goes through Q1, that only Q1 changes its polarization. But polarization is a property of the wave, not of the particle. The wave goes through both slits and should be added at the detector position. The result is not different for particles going through the blue or red slit. Therefore it is still not possible to measure the path of the particle.

2b Still the interference disappears, so why? The article does remark that the output of 3 + 4 = 2, but it does not draw the obvious conclusion: the interference pattern does not disappear, but there are now two patterns, 180º shifted, which added looks like no interference.

3-4a The interference pattern of 3 and 4 differ 180º. This will happen when Q1 and Q2 shift the phase 90º in opposite direction. This agrees with the angle of POL and the behaviour of quarter wave plates. If the polarization of the incoming wave is parallel to one of the axes, the output polarization will not rotate, but only shift the phase 90º:

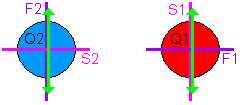
Above is a view from Ds to the slits and Q1/Q2. If the incoming polarization is vertical then there is no horizontal component, so no rotation of the outgoing polarization. Only S is delayed 90º compared to F. With horizontal incoming polarization it is the other way around. Indeed the article describes that in 3 and 4 the POL is set to the F axis of Q1 or Q2 and it is conformal with the measured interference.

3-4b This shows that the detection time in Dp is not crucial. This explains that a position of Dp at longer distance then Ds (the so-called delayed erasure) makes no difference. It is the behaviour of POL together with Q1/Q2 which determines the interference pattern.

So the conclusion should be that there is no marking of the particle, no erasing, so no delayed erasing.

 

[Cthugha]

Few comments:

1 Without Q1/2 and POL there was an interference pattern in Ds

I suppose you mean the right thing, but precise language is important when discussing this experiment. There is an interference pattern in coincidence counts between Ds and Dp, but not on Ds alone.

2a The idea is that if the particle goes through Q1, that only Q1 changes its polarization. But polarization is a property of the wave, not of the particle. The wave goes through both slits and should be added at the detector position. The result is not different for particles going through the blue or red slit. Therefore it is still not possible to measure the path of the particle.

That is not correct. Electric fields add vectorially, so orthogonal polarizations do not interfere. At this stage it is possible to measure the path of the particle just by placing a polarizer in front of Ds which only allows one of the two polarizations to pass. This will only let the field which went through one of the slits pass through. Note that it does not matter, whether you actually place the detector there. The mere possibility of doing it at the position where the detection takes places is sufficient.

 

[DParlevliet]

I suppose you mean the right thing, but precise language is important when discussing this experiment. There is an interference pattern in coincidence counts between Ds and Dp, but not on Ds alone.

Indeed I suppose so in this measurement. But I think it will not differ, because from all photons detected in Ds the entangled photons will be detected in Dp.

That is not correct. Electric fields add vectorially, so orthogonal polarizations do not interfere. At this stage it is possible to measure the path of the particle just by placing a polarizer in front of Ds which only allows one of the two polarizations to pass. This will only let the field which went through one of the slits pass through. Note that it does not matter, whether you actually place the detector there. The mere possibility of doing it at the position where the detection takes places is sufficient.

With "added" I mean taking into account orthogonal. But the point is that the sum, whatever it is, does not differ if the particle goes through one or the other slit. So detector Ds cannot measure which path the photon followed. If you place a polarizer you just block polarization from one slit. But still the particle can goes through each slit. The particle has no polarization.

 

[Cthugha]

Indeed I suppose so in this measurement. But I think it will not differ, because from all photons detected in Ds the entangled photons will be detected in Dp.

No, they will not be and that is one of the most important points of the experiment. The slit in front of Dp is only 300 micrometers wide, so actually just a small part of the photons detected at Ds will see the partner detected at Dp. In fact, if you move Dp around, you are able to change the interference pattern in the coincidence counts.

Assuming that doing coincidence counting is just some trick to reduce noise or something similar is the main fallacy behind many misconceptions about the entangled photons created from BBOs or similar sources. The two-photon probability amplitudes are absoluteley fundamental and coincidence counting is the single most important thing to do in such measurements. Measurements in one arm alone are absolutely meaningless.

With "added" I mean taking into account orthogonal. But the point is that the sum, whatever it is, does not differ if the particle goes through one or the other slit. So detector Ds cannot measure which path the photon followed.

Put a polarizer there and you can. It is as simple as that.

 

[DParlevliet]

Put a polarizer there and you can. It is as simple as that.

If Q1/Q2 are mounted as above, what will the polarization be at Ds in case the particle goes through one or the other slit?

 

[Cthugha]

If Q1/Q2 are mounted as above, what will the polarization be at Ds in case the particle goes through one or the other slit?

That depends on the initial polarization of the particle before the double slit. A QWP that has the optical axis oriented at 45 degrees to the polarization axis of the light beam will turn horizontally polarized light into circularly polarized light, either clockwise or counterclockwise - that depends on whether you place it at +45 degrees or -45 degrees. For vertically polarized light, it is the other way round. For any other linear polarization a QWP will produce elliptically polarized light. However, if you write down the Jones vectors for the light fields created by some fixed linear polarization going through
a) a QWP at some orientation
b) a QWP oriented at 90 degrees to the first one
you will always find that the two fields that arise are orthogonal.

That means that if you now place a polarizer at Ds, you can get different results, depending on how it is oriented: You can get no interference pattern at all (orientation such that only light from one slit passes through), you can get fringes (superposition of both paths) or antifringes (superposition of both paths, but different relative phase). Using the latter orientations also means erasing which-way-information (now in a classical setup). However, without the polarizer the which-way info is always present as the fields are orthogonal.

 

[DParlevliet]

That depends on the initial polarization of the particle before the double slit.

Let us take an easy example: Suppose the photon (not the particle) is polarized as above, parrallel to the fast axis of Q2.

 

[Cthugha]

Let us take an easy example: Suppose the photon (not the particle) is polarized as above, parrallel to the fast axis of Q2.

I do not get your point. Is the photon not a particle?

Anyway, that is a very different example. The previous discussion was aimed at the state given in the paper, where the photon pair creates a Bell state and you ensure that the QWPs are always at +/-45 degrees to the polarization of the incoming photon.

The case of a well defined polarization parallel to the fast axis of Q2 is pretty boring. Consider the interference pattern you get without having any quarter wave plates inserted. Now by inserting the two quarter wave plates, you just delay the phase of the light field by a fixed amount at Q2 and the same fixed amount +pi/2 at Q1. What you will get is the same polarization as before, but a shifted interference pattern. You will get an interference pattern shifted the other way if you instead have a well defined polarization along the slow axis of Q2. You will get no interference pattern at 45 degrees.

 

[DParlevliet]

I do not get your point. Is the photon not a particle?

No, the photon is a particle and a wave. The particle is a part of the photon properties.

The case of a well defined polarization parallel to the fast axis of Q2 is pretty boring. Consider the interference pattern you get without having any quarter wave plates inserted. Now by inserting the two quarter wave plates, you just delay the phase of the light field by a fixed amount at Q2 and the same fixed amount +pi/2 at Q1. What you will get is the same polarization as before, but a shifted interference pattern.

Right, and is that different if the particle goes through another slit? So how could you measure through which slit the particle went? (the wave goes through both slits).

 

[vanhees71]

No, the photon is a particle and a wave.

Again no! The photon is neither a particle nor a wave (whatever you mean by the latter, I guess a classical wave field). It's a "one-particle Fock state" of the free electromagnetic quantum field.

 

[Cthugha]

No, the photon is a particle and a wave. The particle is a part of the photon properties.

As has already been pointed out, the notion of particle-wave duality is pretty outdated. All the quantities of interest - no matter whether the layman would consider them wave-like or particle-like from a naive point of view - can be derived from a single, absolutely consistent formulation.

Right, and is that different if the particle goes through another slit? So how could you measure through which slit the particle went? (the wave goes through both slits).

I do not get your point. Let me try to understand. The difference between a light field with polarization aligned with the fast or slow axis of a QWP (just a phase shift) and a light field polarized at 45 degrees to the fast/slow axis (polarization conversion from linear to circular) is clear? In the latter case some spin angular momentum of +/- hbar is transferred to the photon. This is measurable.

 

[DParlevliet]

The case of a well defined polarization parallel to the fast axis of Q2 is pretty boring. Consider the interference pattern you get without having any quarter wave plates inserted. Now by inserting the two quarter wave plates, you just delay the phase of the light field by a fixed amount at Q2 and the same fixed amount +pi/2 at Q1. What you will get is the same polarization as before, but a shifted interference pattern.

What I mean is that above you describe the wave at the detector to be the sum of two waves which differ in phase +pi/2 (suppose the detector is in the middle). Was the photon in that explanation going through Q1 or Q2? Would it be different if the photon went through the other slit? (we are talking about a single photon).

 

[Cthugha]

What I mean is that above you describe the wave at the detector to be the sum of two waves which differ in phase +pi/2 (suppose the detector is in the middle). Was the photon in that explanation going through Q1 or Q2? Would it be different if the photon went through the other slit? (we are talking about a single photon).

I still do not get what you are aiming at. In the case of alignment along the fast or slow axis you do not get which way information, but that is unrelated to the double slit quantum eraser where you are always at 45 degrees to the optical axis and therefore do not just have a simple phase shift, but also polarization change and transfer of spin orbital momentum. The two cases are fundamentally different.

 

[DParlevliet]

At this stage it is possible to measure the path of the particle just by placing a polarizer in front of Ds which only allows one of the two polarizations to pass. This will only let the field which went through one of the slits pass through.

Alright, then at 45 degrees. At the detector Ds now two waves add up (from both slits) which are rotating left and right. How does the result differ if the photon is going through one or the other slit?

Or in your above argument: the polarizer will only let the field which went through one of the slits pass through. But how does that relate to which slit the particle went through? If the particle passed through slit 1, its wave is going through both slits. If it passed slit 2, again its wave goes through both slits.

 

[Cthugha]

Alright, then at 45 degrees. At the detector Ds now two waves add up (from both slits) which are rotating left and right. How does the result differ if the photon is going through one or the other slit?

As I wrote earlier: Going through the QWP transfers spin angular momentum to the photon. If you perform a measurement of the spin angular momentum of the photon, you can clearly say which way it went.

Or in your above argument: the polarizer will only let the field which went through one of the slits pass through. But how does that relate to which slit the particle went through? If the particle passed through slit 1, its wave is going through both slits. If it passed slit 2, again its wave goes through both slits.

I do not get your focus on wave things. QM is based on a wave-like formalism and of course you consider all the paths and probabilities when calculating detection probabilities and averages. Besides calculating probabilities, how is the "wave" relevant for anything that happens in a single run of the experiment?

As soon as - in an otherwise fixed experimental geometry - you can perform a measurement at the position of the final detector which allows you to identify subsets which can only correspond to slit A or B, you have path information. If you have interference and no path interference such a measurement is not even possible in principle.

 

[DParlevliet]

As I wrote earlier: Going through the QWP transfers spin angular momentum to the photon. If you perform a measurement of the spin angular momentum of the photon, you can clearly say which way it went.

How do you measure spin?

 

[Cthugha]

There are several ways. The boring one consists of another QWP and a polarizer, but I suppose this is not what you want to hear.

You can put a small, light, frictionless disk there. If it absorbs the photon, the angular momentum gets transferred to the disk and it will start to rotate, either clockwise or counterclockwise, depending on the spin.

Or you can put a detector based on some spin-sensitive absorption path there. Consider for example the ground state of a quantum dot (artificial atom). The carriers there are excitons, bound electron-hole pairs usually consisting of electrons of spin +/- 1/2 and heavy holes with spin +/- 3/2. Due to Fermi exclusion only two of those pairs fit into the ground state. One with electron spin + 1/2 and hole spin - 3/2 (total spin -1) and one with electron spin -1/2 and hole spin +3/2 (total spin +1). Other combinations are not optically active. Now these pairs with spin +/- 1 can be created by absorption of a photon of matching spin. If you now insert polarized electrons and holes into the system, you can get a quantum dot, where one of the two electron-hole pairs is always present and the other is not. Accordingly only photons with one kind of spin can be absorbed

 

[DParlevliet]

There are several ways. The boring one consists of another QWP and a polarizer, but I suppose this is not what you want to hear.

I like the borings ones, because they better show what is happening. QWP and polarizer act on waves, so we are back again to waves and the question: how do the (sum of two) waves look like when the particle is going through Q1 or Q2? In what way do they differ?

You can put a small, light, frictionless disk there. If it absorbs the photon, the angular momentum gets transferred to the disk and it will start to rotate, either clockwise or counterclockwise, depending on the spin.

My answer on the question above: Q1 and Q2 cause polarization clockwise and anti-clockwise. So if they add up at the detector, there is no rotation anymore, so no spin.

 

[Cthugha]

I like the borings ones, because they better show what is happening. QWP and polarizer act on waves, so we are back again to waves and the question: how do the (sum of two) waves look like when the particle is going through Q1 or Q2? In what way do they differ?

We are going in circles here. The combination of QWP and polarizers will only let one of the fields pass.

My answer on the question above: Q1 and Q2 cause polarization clockwise and anti-clockwise. So if they add up at the detector, there is no rotation anymore, so no spin.

There is no average spin transfer if you repeat the experiment many times under the same initial conditions. But every single time you do a single experimental run, there will be absorption of one photon and spin will be transferred. The incoherent addition of the "waves" is important for averaging over many runs, for any single repetition it just gives you probabilities for what will happen. That is like having two doors and 50% of the people going through the left one and 50% going through the right one. The average "wave person" would then go through the wall in the middle of the two doors. Averages do not have a 1 to 1-relationship to the single repetition of the experiment.

 

[DParlevliet]

But every single time you do a single experimental run, there will be absorption of one photon and spin will be transferred.

But as mentioned above, when both waves from each QWP combine again (add up) there is no spin anymore. If you add up the clockwise wave from Q1 and the anti-clockwise wave from Q2 at the position of absorption, the result is no-spin.

 

[Cthugha]

That is a very bad misconception. Are you talking about, say, representing linear polarization as a superposition of left and right circularly polarized light? This coherent addition is possible (not really in a double slit where the two beams arrive at an angle, though), but one has to be careful with the meaning.

Photons are spin 1 particles. On every single photon detection a spin of +/-1 is transferred to the detector. There is no way around that and there are no spin 0 photons. Still one can get linearly polarized single photon states with spin 0, which does not seem to fit. One has to consider that a single photon state is intended to describe an ensemble of identically prepared single photons. In a linearly polarized single photon state you get an equal 50%/50% probability to have a spin of +1 or -1 transferred to the detector upon detection and there is no way to know what will happen beforehand.

What you do is trying to apply classical wave reasoning to single photons. This is not a valid picture and one of the reasons why the term "wave-particle-duality" is so outdated. It led people to believe that there is a classical wave aspect to photons. It is not. We are not discussing classical electromagnetic fields here for photons. The "wavey" things are probability amplitudes and have a very different meaning.

 

[DParlevliet]

But the result is the same. When on the detector the circular polarizations of the waves from both slits add up, the result is lineair polarization, so the state of "50%/50% probability to have a spin of +1 or -1 transferred to the detector upon detection and there is no way to know what will happen".

 

[Cthugha]

That is incorrect. You can call it collapse or decoherence or use a similar concept. You may be lucky to keep the superposition alive for a very short while after absorption by exciting a superposition of electrons with spins +1 and -1, but this is more or less never really the case. However, even if so, these interact strongly with their surroundings, cause decoherence and leave you with either a spin up or spin down electron. Superpositions do not survive measurements. Have a look at the kind of electron you get and you know which slit the photon went through.

 

[DParlevliet]

What is incorrect? If you add two waves with opposite circular polarization (and equal amplitude) , the result is a lineair polarization?

 

[Cthugha]

What is incorrect? If you add two waves with opposite circular polarization (and equal amplitude) , the result is a lineair polarization?

This is what happens if you add two CLASSICAL waves (in a certain geometry). We were discussing single photons. It does not work that way for single photons. You can add probability amplitudes. That is very different. vanhees71 already pointed that out.

See e.g. this summary of a paper on single photons with arbitrary waveform (Phys. Rev. Lett. 109, 053602 (2012)) for another take on that:
http://physics.aps.org/articles/v5/86

They say explicitly:
A pulse of light can have almost any shape in space and in time, determined by the amplitudes and phases of its frequency components. Surprisingly, single photons can also be generated in a variety of complex shapes. The difference is that the amplitude for a single photon doesn’t represent a definite value of the electric field strength; instead it’s associated with the probability of detecting the photon at each location and time.

 

[DParlevliet]

They also say "..in the same way that it is done classically"
We start with a single photon with classical polarization, we describe the rotation in the QWP with classical wave phase shift, then it is diffracted as Huygens calculated for waves. And now finally I add them in a classical way and that is not allowed?
You can calculate with QM math, but if one chooses the classical way it should fit too. If not, then something is wrong.
You may doubt the wave-particle-duality, but that is still mentioned in every book I read, everywhere in Wikipedia, on sites of universities and a part of the Copenhagen interpretation. So it still is the majority view in the scientific world.

But then the proof: do you know of publications where this measuring of which path after QWP has been actually done?

 

[Cthugha]

They also say "..in the same way that it is done classically"

"The optimized detection scheme is “pure and simple coherent control in the same way that it is done classically"

You realize that this is unrelated to the question of whether you can treat photons classically?

We start with a single photon with classical polarization

Stop! No. Again: It does not work like that for single photons. See my last post for the reasons. You get a probability amplitude for detecting a photon when you perform a polarization-sensitive measurement. That is it.

, we describe the rotation in the QWP with classical wave phase shift, then it is diffracted as Huygens calculated for waves. And now finally I add them in a classical way and that is not allowed?

You add probability amplitudes. That is a different thing with a different meaning.

You can calculate with QM math, but if one chooses the classical way it should fit too. If not, then something is wrong.

No. If one could calculate this classically it would mean that quantum mechanics is unnecessary. You cannot discuss single photons without qm.

You may doubt the wave-particle-duality, but that is still mentioned in every book I read, everywhere in Wikipedia, on sites of universities and a part of the Copenhagen interpretation. So it still is the majority view in the scientific world.

What people consider wave-particle duality today has nothing to do with what you think it is. See the wikipedia entry saying
"When viewed through this formalism, the measurement of the wave function will randomly "collapse", or rather "decohere", to a sharply peaked function at some location. The likelihood of detecting the particle at any particular location is equal to the squared amplitude of the wave function there." and "Following the development of quantum field theory the ambiguity disappeared. Although there is still debate as to whether one should accept the field as "real", the debate over using the term wave or particle is rendered meaningless. The field permits solutions that follow the wave equation, which are referred to as the wave functions. The term particle is used to label the irreducible representations of the Lorentz group that are permitted by the field. An interaction as in a Feynman diagram is accepted as a calculationally convenient approximation where the outgoing legs are known to be simplifications of the propagation and the internal lines are for some order in an expansion of the field interaction. Since the field is non-local and quantized, the phenomena which previously were thought of as paradoxes are explained."

The part about the field being non-local and quantized is the important one. This is not the classical field you have in mind when you talk about a field.

By the way, these forums even have a FAQ entry on that question: https://www.physicsforums.com/showthread.php?t=511178

But then the proof: do you know of publications where this measuring of which path after QWP has been actually done?

The double slit quantum eraser does it. It is done in "Quantum mechanical which-way experiment with an internal degree of freedom" (Nature Communications 4, 2594 (2013)) with a different experimental geometry. There are way more, but none I can access right now from home.

 

[DParlevliet]

You add probability amplitudes..

Indeed I do. Of propability waves. And the polarization of thess waves are right and left rotating after Q1 and Q2. And after adding at the detector lineair again?

 

[Cthugha]

And after adding at the detector lineair again?

Let me ephasize one aspect of the wikipedia article again:
"When viewed through this formalism, the measurement of the wave function will randomly "collapse", or rather "decohere", to a sharply peaked function at some location."

Linear polarization is an equal and phase-stable superposition of left-circular and right-circular. However, a measurement - say absorption by a photon - will leave the system in an eigenstate. Photons are spin 1 particles. A single photon must have exactly 1 unit of spin angular momentum. Not 0, not 2. A linear state has spin zero. The collapse/decoherence process can therefore only lead to a state consistent with the photon being circularly polarized.

If you add the probability amplitudes to get a linear state, therefore you need to interpret that as having a 50/50 probability to have one or the other happening, but in a single absorption event you will always transfer a single quantum of spin angular momentum, not 0 as would be the case if linearly polarized single photons (as contrasted to single photon states) existed which are not a superposition.

You can do all the math and add up the waves, but you must be aware that the physics behind the math needs to be interpreted very differently when discussing problems that need qm treatment.

 

[DParlevliet]

Alright, I will, so suppose I was right, including "lineair" is 50/50%.
Now your spin explanation:
- Before Q1/Q2, is the spin of the photon + or -
- Suppose after Q1 the spin is +, what is the spin after Q2?

 

[Cthugha]

Now your spin explanation:
- Before Q1/Q2, is the spin of the photon + or -
- Suppose after Q1 the spin is +, what is the spin after Q2?

Sorry. I do not know which scenario you are talking about. Q1 and Q2 are at 90 degrees to each other? At what orientation are they relative to the incoming photon and what is its polarization?

 

[DParlevliet]

The scenario we are discussing about: axis Q1 and Q2 at 90 degrees, and 45 degree to the incoming photon with lineair polarization.

 

[Cthugha]

Ok, 45 degrees. So let us choose the initial polarizatiion such that we get left circular polarization (-) after Q1 and right circular polarization (+) after Q2.

At a position at the deetctor these overlap. As they overlap at some angle, you do not really get a linear polarization, not even classically, but let us ignore that for a moment. In qm you now add the probability amplitudes and then square them to get the probabilities for the possible detection events. The detection events of course rely on absorption. In absorption events, conservation of energy, momentum and angular momentum must be satisfied, so the electron or whatever particle absorbs the single photon needs to acquire all of them. Photons have an energy of $\hbar \omega$, spin angular momentum of $\pm \hbar$ and linear momentum of $\hbar k$. Electrons decohere quickly, so after the absorption, you will find it in an eigenstate in which it gained these amounts of energy and momentum. This includes the $\pm \hbar$ of spin angular momentum. As only these values are possible, you can easily check which amount was given to the electron and this automatically tells you, whether the photon was - or + and also which path it took. Both processes just take place with equal probability.

 

[DParlevliet]

We would no talk about waves anymore (that was my area) but about your explanations with spin.
- I suppose in your explanation after Q1 the spin is -, and after Q2 + ?
- Now what is the spin before Q1/Q2 ?

 

[Cthugha]

- Now what is the spin before Q1/Q2 ?

You wanted to have the quantum equivalent of linear polarization. That means that in the ensemble you have a coherent, fixed-phase superposition of + and -. For the single photon in the experimental run it means that it is essentially undefined at this moment which of the two it is. It is in a superposition, if you want to think about it that way.

It is of course not trivial to create such a state. The problem about conservation rules of course also concerns the emission process. The energy, spin and momentum need to be transferred from the emitter to the photon, so in principle checking the state of the emitter can tell you the state of the photon. Therefore it is important to have some emission process which is more or less not too sensitive to decoherence. For example if the emitter is very light, the recoil from the emission process will already destroy the superposition and you never have it in the first place. If it is heavy, the momentum transfer drowns in uncertainty and the emitter does not end up in a state that is orthogonal to the initial one. That is one of the reasons why non-linear optical processes like parametric downconversion using BBOs are heavily used in quantum optics.