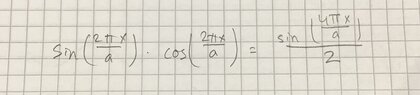SUMMARY
The forum discussion focuses on solving the infinite square well problem in quantum mechanics, specifically addressing the integral in part d) and its relation to the wave function ψ4(x). Users discuss the use of trigonometric identities to simplify the integral involving sin and cos functions. The relationship between the expression ##\frac{\sin\left(\frac{4\pi x}{a}\right)}{2}## and the eigenfunction ##\psi_4(x)## is clarified, emphasizing the importance of orthonormality in evaluating integrals without explicit calculations.
PREREQUISITES
- Understanding of quantum mechanics, particularly the infinite square well model.
- Familiarity with wave functions and eigenfunctions, specifically ##\psi_n(x)##.
- Knowledge of trigonometric identities and their application in integrals.
- Basic principles of orthonormality in quantum mechanics.
NEXT STEPS
- Learn about the properties of eigenfunctions in quantum mechanics.
- Study the application of orthonormality in evaluating integrals involving wave functions.
- Explore trigonometric identities and their use in simplifying integrals in physics.
- Investigate the infinite square well problem further, focusing on different potential energy functions.
USEFUL FOR
Students and professionals in physics, particularly those studying quantum mechanics, as well as educators looking for insights into solving complex integrals related to wave functions.