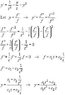Question about a Riccati type diff eq.

[kenano]

\acute{y} = \frac{1}{t^{2}} -\frac{y}{t} - y^{2}

To solve a Riccati type diff eq a particular solution is needed. In our case it is: y_{1} = -\frac{1}{t}

By setting
y= y_{1}+\frac{1}{u}= -\frac{1}{t}+\frac{1}{u}

and differentiating this
\acute{y}= \frac{1}{t^{2}}-\frac{u'}{u^{2}}

Substituting for y and y' in the first original equation:
\frac{1}{t^{2}}-\frac{u'}{u^{2}}= \frac{1}{t^{2}}-\frac{1}{t}(-\frac{1}{t}+\frac{1}{u})-(-\frac{1}{t}+\frac{1}{u})^{2}

This yields the general solution:
y= -\frac{1}{t}+\frac{1}{\frac{t}{2}+\frac{K}{t}}

(K being a constant)

But, according to the general solution above, it isn't possible to have a particular solution:
y_{1}= -\frac{1}{t}
since we can't have the second term at the right-hand side zero.

So, am i missing something?

Thanks for help in advance.

 

[JJacquelin]

To solve a Riccati type diff eq a particular solution is needed

Not necessarily.
Often it is easier to transform the Riccati ODE into a second order linear ODE which can be solved without knowing a particular solution.

 

[kenano]

Thank you for your answer Jacquelin. I still have some questions.

-We have two constants in the solution to a first order equation because of the intermediate second order diff eq. But the original eq is a first order one. Then how could the second constant be determined in a boundary value problem? Or one of them is zero automatically?
-It seems that we still cannot have the particular solution y1=-1/t according to new solution. Does it mean it is a singular solution?
-How did you solve the intermediate second order diff eq with variable coefficients without series expansion?

 

[JJacquelin]

We have two constants in the solution to a first order equation because of the intermediate second order diff eq. But the original eq is a first order one. Then how could the second constant be determined in a boundary value problem? Or one of them is zero automatically?

In fact there is only one constant in the solution (due to the proportional relationship y=f'/f )
Let c=c1/c2 and rewrite the general solution as :
y = (c t²-1)/(t(c t²+1))

It seems that we still cannot have the particular solution y1=-1/t according to new solution. Does it mean it is a singular solution?

No, we can have the solution y1=-1/t . It corresponds to the case of c=0.

How did you solve the intermediate second order diff eq with variable coefficients without series expansion?

The intermediate linear second order ODE f''+(1/t)f'-(1/t²)f=0 is homogeneous. So, referring to the usual method, the characteristic equation corresponding to solutions of the form t^k is :
k(k-1)+k-1=0 which roots are k=1 and k=-1 so, the solution of the ODE is :
f = c1 t + c2 / t

 

[kenano]

Now it's all clear. Thank you very much.

 

[JJacquelin]

This was a particular case of Riccati equation.
The general Riccati ODE :
y'' = p(x) + q(x) y + r(x) y²
is tansformed into a second order linear ODE by :
y = -(1/r) f ' / f
where f(x) is the unknown function.

Of course, this transformation has interest only if the second order linear ODE is easy to solve directly, thanks to convenient classical methods : a lot have known solutions with elementary functions or with well-known special functions.