Question about a rigid body and energy

[Clara Chung]

Homework Statement

Homework Equations

The Attempt at a Solution

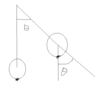
I have posted the solution, but I don't really understand about the second term in the equation.
Shouldn't the angular velocity of the ball be (b dθ/dt) /a instead of ( (b-a) dθ/dt )/a in the solution?

 

[timetraveller123]

if i am not wrong the nonslip condition implies that
$v_{cm} = \omega a\\ v_{cm} = (b-a)\dot \theta$
hence the equation

 

[Clara Chung]

if i am not wrong the nonslip condition implies that
$v_{cm} = \omega a\\ v_{cm} = (b-a)\dot \theta$
hence the equation

Thank you, but I still don't understand. The ball touches the sphere. If the angle displace is \theta, the ball's circumference undergone a distance of b \theta.

 

[timetraveller123]

i think it is any rigid body motion can be described as translation and rotation about a point
i think in principle any other can be used but getting its translation velocity will be hard(i think not sure) but for cm it is quite easy it is always b-a away from centre hence the bottom most point is translating at the velcoity
vcm forward but rotating backward at omega r you set them equal to each other for non slip

 

[Clara Chung]

i think it is any rigid body motion can be described as translation and rotation about a point
i think in principle any other can be used but getting its translation velocity will be hard(i think not sure) but for cm it is quite easy it is always b-a away from centre hence the bottom most point is translating at the velcoity
vcm forward but rotating backward at omega r you set them equal to each other for non slip

I am not sure if vcm = wa

 

[timetraveller123]

when the ball is rolling , the velocity of point in contact with the sphere can be described as translation of the center of mass and the rotation about cm the sum of the two must be zero .
the translation is vcm and the rotation velocity about cm is w times distance which is w a
i could not find a link for ball rolling within ball but i found one for ball rolling on top of r
here vcm is r+R away and at 3:20 he write w = v/r

 

[PeroK]

Thank you, but I still don't understand. The ball touches the sphere. If the angle displace is \theta, the ball's circumference undergone a distance of b \theta.

You need to draw a good diagram of the situation and look very closely at how many times the small sphere rotates as it moves all the way round the inside of the larger sphere. For example, you could take the small sphere to have 1/4 of the radius of the large sphere.

 

[Clara Chung]

You need to draw a good diagram of the situation and look very closely at how many times the small sphere rotates as it moves all the way round the inside of the larger sphere. For example, you could take the small sphere to have 1/4 of the radius of the large sphere.

Sorry I just can't get the idea, maybe I am too stupid.
If the centre of the small ball travel by theta. The circumference of the small ball has traveled a distance of bθ.
Therefore the angle traveled by the small ball is Φ=bθ/a.
By differentiating, I can get
w=dΦ/dt = b/a dθ/dt.

 

[PeroK]

Sorry I just can't get the idea, maybe I am too stupid.
If the centre of the small ball travel by theta. The circumference of the small ball has traveled a distance of bθ.
Therefore the angle traveled by the small ball is Φ=bθ/a.
By differentiating, I can get
w=dΦ/dt = b/a dθ/dt.

It's not a question of being stupid. But, that is nothing to do with what I posted. It's not a question of differentiation. It's a question of figuring out a tricky physical scenario.

I'll give you some help:

You need to draw a good diagram of the situation and look very closely at how many times the small sphere rotates as it moves all the way round the inside of the larger sphere. For example, you could take the small sphere to have 1/4 of the radius of the large sphere.

In this scenario, the small sphere does not rotate 4 times as it rolls around inside the larger sphere. You need to figure out how many times it does rotate and why.

 

[PeroK]

PS in the above diagram, mark the point on the small sphere which starts at the bottom, touching the large sphere. Imagine the small sphere rolling thru one quarter of the large sphere. Where is the mark on the small sphere? How much has the small sphere rotated in rolling 1/4 of the way round the large sphere?

 

[Clara Chung]

PS in the above diagram, mark the point on the small sphere which starts at the bottom, touching the large sphere. Imagine the small sphere rolling thru one quarter of the large sphere. Where is the mark on the small sphere? How much has the small sphere rotated in rolling 1/4 of the way round the large sphere?

Does the point land on the rightmost of the sphere?

 

[PeroK]

Does the point land on the rightmost of the sphere?

Yes. And that's less than one rotation of the small sphere.

 

[Clara Chung]

Yes. And that's more than one rotation of the small sphere.

Does it rotate 3/4 cycle (less than one rotation)? What does it mean by a rotation, is it when the point is again in the buttom position?

 

[PeroK]

Does it rotate 3/4 cycle (less than one rotation)? What does it mean by a rotation, is it when the point is again in the buttom position?

Yes, less than one rotation. What that means is that you have one angle representing how far round the large sphere the small sphere has rolled. Let's call this $\phi$. And another angle representing the angular rotation of the small sphere. Let's call this $\theta$.

In this case, we have $\theta = 3 \phi$. And, in general, we have $\theta = \frac{b-a}{a}\phi$.

You also know how far the centre of mass of the small sphere has moved. It is moving in a circle of radius $4-1$ units. And, in general, of radius $b-a$.

These two things give you the KE of the rolling sphere.

PS I tried to get $\phi$ and $\theta$ the right way round, but of course the book has them the other way round. Apologies.

 

[Clara Chung]

Yes, less than one rotation. What that means is that you have one angle representing how far round the large sphere the small sphere has rolled. Let's call this $\phi$. And another angle representing the angular rotation of the small sphere. Let's call this $\theta$.

In this case, we have $\theta = \frac34 \phi$. And, in general, we have $\theta = \frac{b-a}{a}\phi$.

You also know how far the centre of mass of the small sphere has moved. It is moving in a circle of radius $4-1$ units. And, in general, of radius $b-a$.

These two things give you the KE of the rolling sphere.

Thank you for your help

 

[timetraveller123]

@PeroK
i was thinking about the problem as a sum of translation and rotation

so first i imagined it being frictionless in this case when when the centre is displaced theta the initial point of contact also is rotated by theta from the final point of contact

hence the point which is always is contact with the sphere has moved by b theta but the smaller circle will have appeared to have rotated by a theta
when friction is turned on friction will make the smaller circle turn an additional angle phi to make the translational and rotational distance equal
so b theta = a theta + a phi differentiating yields the necessary expression
is this valid to do it?

 

[PeroK]

@PeroK
i was thinking about the problem as a sum of translation and rotation

so first i imagined it being frictionless in this case when when the centre is displaced theta the initial point of contact also is rotated by theta from the final point of contact
View attachment 231468

hence the point which is always is contact with the sphere has moved by b theta but the smaller circle will have appeared to have rotated by a theta
when friction is turned on friction will make the smaller circle turn an additional angle phi to make the translational and rotational distance equal
so b theta = a theta + a phi differentiating yields the necessary expression
is this valid to do it?

Yes, I think that's another way to look at it.

 

[timetraveller123]

ok thanks