voila
- 58
- 6
Hi. I'm taking a look at some lectures by Charles Kane, and he uses this simple model of polyacetylene (1D chain of atoms with alternating bonds which give alternating hopping amplitudes) [view attached image].
There are two types of polyacetylene topologically inequivalent. They both give the same band structure, but on one the Bloch function acquires a Berry phase of pi when going through the Brillouin zone, whereas the other doesn't.
In the very next slide, it's discussed how attaching both types of topologically inequivalent chains gives rise to a topologically protected closing of the energy gap on the frontier of the BZ because when going from one to another your d(k) is going to have to go through zero, which implies delta t, and so the gap, to be also zero.
However, I'm interested in what role the Berry phase plays here. Is it somehow that, as one of the wavefunctions picks a minus sign (Berry phase of pi), there's something like a flipping in the energy band diagram for some kind of continuity reasons? As far as I can see, he mentions the Berry phase in the slide for no reason,
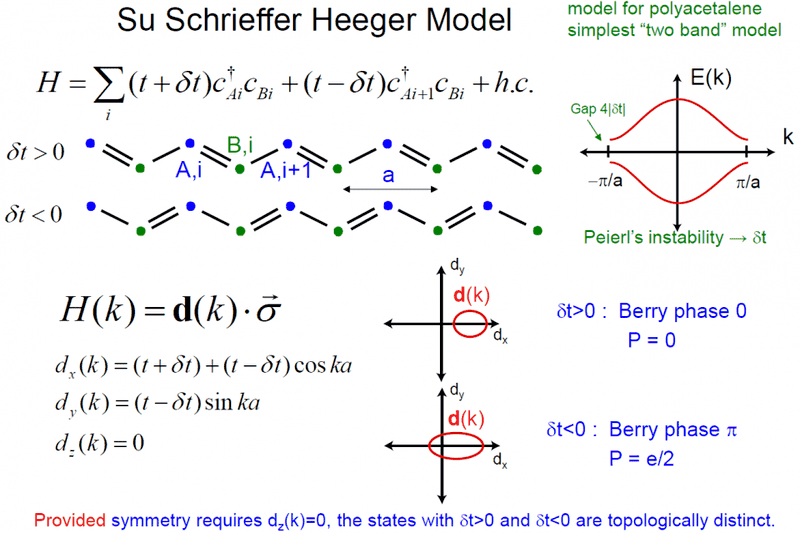
There are two types of polyacetylene topologically inequivalent. They both give the same band structure, but on one the Bloch function acquires a Berry phase of pi when going through the Brillouin zone, whereas the other doesn't.
In the very next slide, it's discussed how attaching both types of topologically inequivalent chains gives rise to a topologically protected closing of the energy gap on the frontier of the BZ because when going from one to another your d(k) is going to have to go through zero, which implies delta t, and so the gap, to be also zero.
However, I'm interested in what role the Berry phase plays here. Is it somehow that, as one of the wavefunctions picks a minus sign (Berry phase of pi), there's something like a flipping in the energy band diagram for some kind of continuity reasons? As far as I can see, he mentions the Berry phase in the slide for no reason,