A Question about dilaton monopole interaction derivation

[user1139]

TL;DR Summary

Please see below.

I am trying to understand how one derives the dilaton monopole interaction. In "Black holes and membranes in higher-dimensional theories with dilaton fields", Gibbons and Maeda mentioned that one could obtain the dilaton monopole interaction as such:

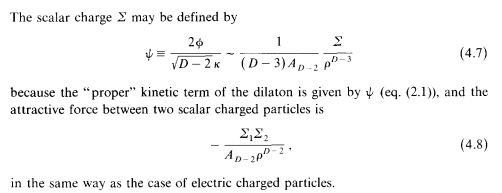
where the action is given by

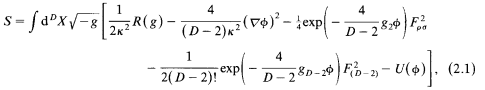
However, I do not understand their reasoning for introducing $\Psi$ to define $\Sigma$ in order to derive Eq. (4.8). Could someone explain it?

 

[mitchell porter]

If you look at the coefficient of (∇φ)² in their equation 2.1, you'll see it's minus the square of the field redefinition factor. So they must be aiming for a dilaton kinetic term with a coefficient of 1.

 

[user1139]

If you look at the coefficient of (∇φ)² in their equation 2.1, you'll see it's minus the square of the field redefinition factor. So they must be aiming for a dilaton kinetic term with a coefficient of 1.

Still, how do they get $\Sigma$ from $\Psi$? Did they just consider the asymptotic behaviour of $\Psi$ and define $\Sigma$ as such?

 

[mitchell porter]

4.7, 4.8 are the same form as 4.5, 4.4, which describe electric charge and electrostatic potential. The reasoning would appear to be exactly analogous.