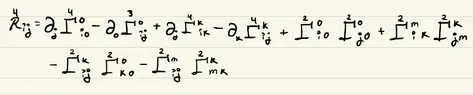SUMMARY
The discussion centers on the exclusion of the fourth-order term of the purely spatial components of the Ricci tensor, denoted as R_{ij}, in Steven Weinberg's General Relativity book, specifically in Chapter 9 regarding the post-Newtonian approximation. Participants clarify that this exclusion is due to the dependency of R_{ij} on affine connection terms not included in the relevant equations (9.1.16) through (9.1.22). The focus is on maintaining a balance between accuracy and computational efficiency, as time components drive dynamics while spatial components serve as corrections. This approach is standard in post-Newtonian theory and is crucial for applications in gravitational wave astronomy and precision tests of General Relativity.
PREREQUISITES
- Understanding of Ricci tensor components in General Relativity
- Familiarity with affine connection terms and their significance
- Knowledge of post-Newtonian approximation techniques
- Basic grasp of gravitational wave astronomy principles
NEXT STEPS
- Study the derivation and implications of the post-Newtonian approximation in General Relativity
- Learn about the role of affine connections in the context of Einstein's field equations
- Explore the mathematical formulation of gravitational wave detection and analysis
- Investigate the significance of the harmonic gauge in simplifying equations in General Relativity
USEFUL FOR
Physicists, particularly those specializing in General Relativity, gravitational wave researchers, and students seeking to deepen their understanding of post-Newtonian approximations and their applications in modern astrophysics.