Gundam404
- 4
- 0
Homework Statement
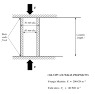
A column has the dimensions shown in the diagram below. (a) What is the minimum length of the column at which buckling is likely to occur? (b) If the column is the length determined in (a), (i) What will be the mode of failure? (ii) At what load would you expect failure to occur?
The specific problem I am having with this question is for b)i) how to determine what the mode of failure will be from the E.S.R. and the S.R. Admittedly this question has been asked many times and people seem to say it will buckle at the length determined in a). Now reading my course material, it states that if your E.S.R is below your S.R. then it will be a crushing mode of failure and above will be buckling. Now I have an E.S.R of 118.741 and a S.R. of 237.52. Am I correct in thinking that this will be a crushing mode of failure with the length of 5.938 m as we have just worked out that the minimum length at which buckling is likely to occur is 5.938 m, so how can this length be the minimum for bucking when the slenderness ratio is 237.52. I would like to make sense of this and I feel like I am chasing my own tail at the moment. Thank you very much for any assistance.
Homework Equations
[/B]
Euler's equation. Fc= ((pi^2)*E*I)/Le^2
E.S.R. = Le/k
S.R. = L/K
The Attempt at a Solution
[/B]
Effective Length = 2.969 m
Length = 5.938 m
k = 0.025
Fc = 306 kN
I = 13.7*10^-7
E.S.R. = 118.741
S.R. = 237.52