Question on 3 circles with changing values

[Jenna_B]

Hey everyone, my friend found this math problem that he couldn't figure out and gave to me. I thought it was quite interesting. So far I haven't been able to find a way to get into it though.

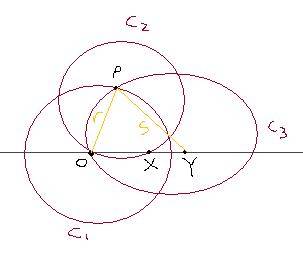
There's a circle, C1, with centre O and radius r. Point Y is anywhere outside the circle. Circle C3 has its centre at Y and its radius is OY. One of its points of intersection with C1 is P.
Another circle, C2, with the same radius as C1, has its centre at P (and thus passes through O).
A line passes through O and Y. C2 has another intersection with this line at X.

Here is an image I made of the problem:

The problem is twofold:
1. Let r = 1; find OX as OY equals 2, 3, and 4 (Find a general statement).
2. Let OY = 2; find OX as r = 2, 3, and 4 (Find a general statement).

Basically you need to find the value of OX as r and OY change, and find a formula for it. Can anyone suggest anything?

EDIT: I've figured out that triangles YOP and PXO are similar...maybe this will lead somewhere.

 

[zgozvrm]

There seems to be a problem with the 2nd part of the problem.
If we let OY = 2 and r = 2, then we break the given rule that Y must lie outside circle 1.
If we let r = 3 or 4, then Y lies inside circle 1.
If we let OY = 2 and r = 4 then circle 2 is the same as circle 3.

 

[I like Serena]

Welcome to PF, Jenna_B! Here's a possible way to solve this.First you need to realize which distance are equal.

Since you circle C2 has its center in P and intersects at O and at X, this means that:
r = OP = PX.
So OPX is an isosceles triangle with sides r, r, and OX.

Circle C3 has its center in Y and intersects at O and at P, meaning:
s = OY = PY.
So OPY is also an isosceles triangle with sides s, s, and r.
Now let's take a look at the angle between OP and OY (which is the same angle as between OP and OX).
Let's call it alpha.

Do you know what the cosine of alpha is?
Look at triangle OPX as well as OPY.

From this you should be able to find a general statement...

 

[zgozvrm]

You are right about the triangles being similar.
Find the cosine of $\angle POY$ as related to each triangle.
You should find the answer.

 

[Jenna_B]

Hey guys, thanks for all the replies!

I found a general formula but it wasn't the correct one; it only seemed to work for r=1. I was told by my teacher that the actual formula is r^2/OY, but I don't see a way that I could derive that...

For reference, my formula is OX = √((2r^2)(1-(cos(2cos^-1(r/OY)))))

EDIT: I got it, you simply had to equate CosPOY with the two triangles >.> Anyways, thanks for all the help guys!