I Question regarding actual computation of tensor at point (Self Study)

[Amateur659]

Hello all,

I am hoping to get some feedback on the manner in which I performed computations towards solving the following problem.

There are a couple specific points which I am not confident of:
1. Did I properly account for the manifold structure in my computation of the nonzero components?
2. Is the general process by which I compute each tensor component correct?

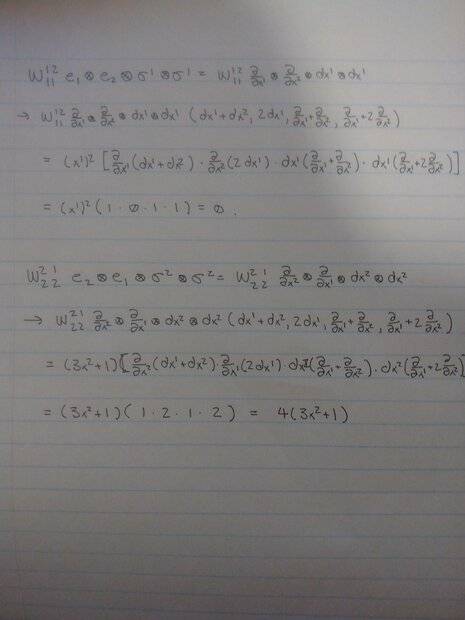
Finally, please let me know if I am making a mistake posting such questions here.

Thank you for your time and feedback!

 

[martinbn]

It looks fine.

 

[Amateur659]

Awesome, thanks for the feedback.