- #1
PainterGuy
- 940
- 69
- TL;DR Summary
- I was trying to understand normal distribution and had a couple of questions.
Hi,
I was watching this Youtube video (please remove the parentheses) :
https://youtu.(be/mtH1fmUVkfE?t=215)
While watching it, a question came to my mind. In the picture, you can easily calculate the total number of customers. It's 1000.
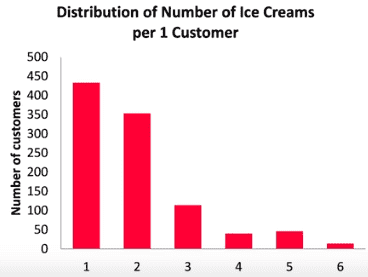
For my question, I'm going to use the same picture. I hope you get the point.
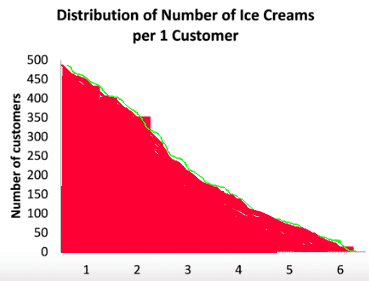
What if the data was continuous something as shown below. How do you calculate the total number of customers? Wouldn't the number be infinite because between any two numbers, e.g. between '2' and '3', there is an infinite set of values? I'm not sure if the question really makes sense.
Could you please guide me?
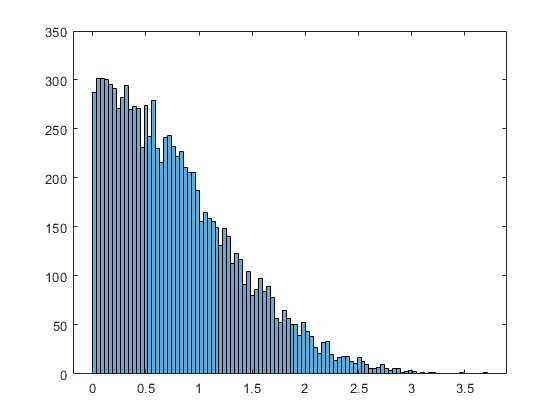
In case of normal distribution the curve also represents continuous data but I believe, practically, it's discrete data made up of very thin slices as shown below and later curve fitting is used to get a continuous curve.
Thank you!
I was watching this Youtube video (please remove the parentheses) :
https://youtu.(be/mtH1fmUVkfE?t=215)
While watching it, a question came to my mind. In the picture, you can easily calculate the total number of customers. It's 1000.
For my question, I'm going to use the same picture. I hope you get the point.
What if the data was continuous something as shown below. How do you calculate the total number of customers? Wouldn't the number be infinite because between any two numbers, e.g. between '2' and '3', there is an infinite set of values? I'm not sure if the question really makes sense.
Could you please guide me?
In case of normal distribution the curve also represents continuous data but I believe, practically, it's discrete data made up of very thin slices as shown below and later curve fitting is used to get a continuous curve.
Thank you!