- #1
PainterGuy
- 940
- 69
Hi,
You could skip these details and find the main question at the bottom. I added the details for the sake completeness and context. Thanks.
Boltzmann distribution of molecular speeds provides an insight into the different speeds the molecules of a gas are moving around with. It provides you with the probability of finding the fraction of molecules moving around with in a certain speed range.
Sometimes a graph as the histogram of data is used for the entire population of molecules and then theoretical curve is used to approximate this data. Since, the molecules are undergoing changing velocity all the time so we can pretend that the distribution is a snapshot taken at one instant of time
The following links illustrate the point.
1: https://en.wikipedia.org/wiki/File:Simulation_of_gas_for_relaxation_demonstration.gif
2: https://chem.libretexts.org/Bookshelves/General_Chemistry/Book:_ChemPRIME_(Moore_et_al.)/09Gases/9.16:_Kinetic_Theory_of_Gases:_The_Distribution_of_Molecular_Speeds
3: https://encrypted-tbn0.gstatic.com/...1eNIvw6VcVdyO5lIGVaOc0EFawkji88A5Jg_Ych4Y0Q90
We can see below that population distribution curve is asymmetric - negatively skewed; it's not normal curve. I believe that they should have used a label "probability" instead of "number of molecules". I'm focusing on the curve with label "low T". Cp is the most probable speed, i.e. modal speed, c_bar is mean speed, c_rms is root mean square speed.
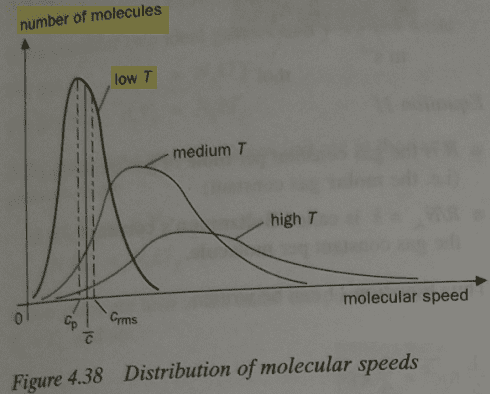
Mathematically, it can be written.

I think it would be relevant to add few comments about probability distribution function, PDF, here.
"In a more precise sense, the PDF is used to specify the probability of the random variable falling within a particular range of values, as opposed to taking on anyone value. This probability is given by the integral of this variable's PDF over that range—that is, it is given by the area under the density function but above the horizontal axis and between the lowest and greatest values of the range. The probability density function is nonnegative everywhere, and its integral over the entire space is equal to one."
Source: https://en.wikipedia.org/wiki/Probability_density_function
A PDF gives area under the curve so just like when you are doing integration you need two limits to find the area and using one value doesn't mean anything.
Watch this video from 4:42 onward to know more about PDF; remove the parentheses:
https://www.youtu(be.com/watch?v=mtH1fmUVkfE)
The following link explains Boltzmann distribution:
https://www.khanacademy.org/science.../a/what-is-the-maxwell-boltzmann-distribution (excellent)
You can find the actual probability density function used here, https://imagizer.imageshack.com/img924/8804/GxnuI2.jpg. It only gives you the probability of speed in one dimensions. The speed in three dimensions is given here, https://imagizer.imageshack.com/img921/2119/BzLs8Q.jpg. This is the source for both images: https://www.tec-science.com/thermod...-the-maxwell-boltzmann-distribution-function/ . Also check this link: https://www.tec-science.com/thermodynamics/kinetic-theory-of-gases/maxwell-boltzmann-distribution/
Question:
Now I'm coming to my question. The provided provided by Maxwell–Boltzmann distribution deals with speed and not velocity. How could I find the number of molecules in a gas traveling in a certain direction with speed between u and u+du where du is an infinitesimal increase in the speed? The speed plus direction is velocity. Thanks for the help.
Note to self:
check related question with picture of molecular speeds: https://www.physicsforums.com/threa...on-discrete-to-continuous.976040/post-6223236
answer: https://www.physicsforums.com/threa...on-discrete-to-continuous.976040/post-6223426
check note to self:
https://www.physicsforums.com/threa...on-discrete-to-continuous.976040/post-6221193https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Map:_Physical_Chemistry_(McQuarrie_and_Simon)/27:_The_Kinetic_Theory_of_Gases/27.3:_The_Distribution_of_Molecular_Speeds_is_Given_by_the_Maxwell-Boltzmann_Distribution
https://chem.libretexts.org/Bookshe...ing_Gas_Properties_to_Kinetic_Theory_of_Gases
https://en.wikipedia.org/wiki/Maxwell–Boltzmann_distributionsolid angle; remove the parentheses: https://www.yout(ube.com/watch?v=RMJucQJ1NGo)
spherical coordinates; remove the parentheses: https://www.youtu(be.com/watch?v=FDyenWWlPdU)
https://hsm.stackexchange.com/quest...ion-of-velocities-in-a-gas-during-an-exam-set
You could skip these details and find the main question at the bottom. I added the details for the sake completeness and context. Thanks.
Boltzmann distribution of molecular speeds provides an insight into the different speeds the molecules of a gas are moving around with. It provides you with the probability of finding the fraction of molecules moving around with in a certain speed range.
Sometimes a graph as the histogram of data is used for the entire population of molecules and then theoretical curve is used to approximate this data. Since, the molecules are undergoing changing velocity all the time so we can pretend that the distribution is a snapshot taken at one instant of time
The following links illustrate the point.
1: https://en.wikipedia.org/wiki/File:Simulation_of_gas_for_relaxation_demonstration.gif
2: https://chem.libretexts.org/Bookshelves/General_Chemistry/Book:_ChemPRIME_(Moore_et_al.)/09Gases/9.16:_Kinetic_Theory_of_Gases:_The_Distribution_of_Molecular_Speeds
3: https://encrypted-tbn0.gstatic.com/...1eNIvw6VcVdyO5lIGVaOc0EFawkji88A5Jg_Ych4Y0Q90
We can see below that population distribution curve is asymmetric - negatively skewed; it's not normal curve. I believe that they should have used a label "probability" instead of "number of molecules". I'm focusing on the curve with label "low T". Cp is the most probable speed, i.e. modal speed, c_bar is mean speed, c_rms is root mean square speed.
Mathematically, it can be written.
I think it would be relevant to add few comments about probability distribution function, PDF, here.
"In a more precise sense, the PDF is used to specify the probability of the random variable falling within a particular range of values, as opposed to taking on anyone value. This probability is given by the integral of this variable's PDF over that range—that is, it is given by the area under the density function but above the horizontal axis and between the lowest and greatest values of the range. The probability density function is nonnegative everywhere, and its integral over the entire space is equal to one."
Source: https://en.wikipedia.org/wiki/Probability_density_function
A PDF gives area under the curve so just like when you are doing integration you need two limits to find the area and using one value doesn't mean anything.
Watch this video from 4:42 onward to know more about PDF; remove the parentheses:
https://www.youtu(be.com/watch?v=mtH1fmUVkfE)
The following link explains Boltzmann distribution:
https://www.khanacademy.org/science.../a/what-is-the-maxwell-boltzmann-distribution (excellent)
You can find the actual probability density function used here, https://imagizer.imageshack.com/img924/8804/GxnuI2.jpg. It only gives you the probability of speed in one dimensions. The speed in three dimensions is given here, https://imagizer.imageshack.com/img921/2119/BzLs8Q.jpg. This is the source for both images: https://www.tec-science.com/thermod...-the-maxwell-boltzmann-distribution-function/ . Also check this link: https://www.tec-science.com/thermodynamics/kinetic-theory-of-gases/maxwell-boltzmann-distribution/
Question:
Now I'm coming to my question. The provided provided by Maxwell–Boltzmann distribution deals with speed and not velocity. How could I find the number of molecules in a gas traveling in a certain direction with speed between u and u+du where du is an infinitesimal increase in the speed? The speed plus direction is velocity. Thanks for the help.
Note to self:
check related question with picture of molecular speeds: https://www.physicsforums.com/threa...on-discrete-to-continuous.976040/post-6223236
answer: https://www.physicsforums.com/threa...on-discrete-to-continuous.976040/post-6223426
check note to self:
https://www.physicsforums.com/threa...on-discrete-to-continuous.976040/post-6221193https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Map:_Physical_Chemistry_(McQuarrie_and_Simon)/27:_The_Kinetic_Theory_of_Gases/27.3:_The_Distribution_of_Molecular_Speeds_is_Given_by_the_Maxwell-Boltzmann_Distribution
https://chem.libretexts.org/Bookshe...ing_Gas_Properties_to_Kinetic_Theory_of_Gases
https://en.wikipedia.org/wiki/Maxwell–Boltzmann_distributionsolid angle; remove the parentheses: https://www.yout(ube.com/watch?v=RMJucQJ1NGo)
spherical coordinates; remove the parentheses: https://www.youtu(be.com/watch?v=FDyenWWlPdU)
https://hsm.stackexchange.com/quest...ion-of-velocities-in-a-gas-during-an-exam-set