Quick logic question,SHM, second order differential equation

[binbagsss]

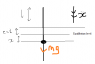
See attached diagram.
Taking downward as postive.
The particle is pulled down past its equiliburm position (e=l) by l/2 and then released.
It has mass m and is subject to a resistive force R.

Why is it that the equation is mg - T - R = ma [1]
as a pose to mg - T + R = ma.[2]

I understand that the tension will oppose mg, however as soon as it is released, it will oscillate upward and so the resistance will be downward, in the same direction as mg .

Or is it a case of the equation being derived at a precise instant in time, and so as it is pulled down , T will act upward, and R will act downward as it is pulled down. So the equation is derived at exactly the point of establishing the system?

However if you chose to establish the equation at the instant of release, when it moves upward and R is therefore downward, would the equation not be (2) - why is this? does T vary after relase also or...

Thanks alot.

 

[Steely Dan]

It would be Equation 2, in the sense that both the resistive force and the gravitational force point in the same direction. There is never any way for Equation 1 to be correct, because the tension and resistive force must always be oppositely directed (assuming by resistive force you do mean a force that always opposes the current velocity).