Quick question about current density

[hahaha158]

Homework Statement

Homework Equations

J=I/A

The Attempt at a Solution

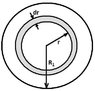
I was just looking at the solution for this, and I was confused because they seemed to use different ways of finding the area. For finding J2, they took the surface area of the end of the cable, pi(r3^2-r2^2), but for finding J2, they took the area to be ∫2pir dr, which i think is the surface area along the inner cable. Why is one using the surface area of the end, and one using the surface area across the outside of an entire cable"?

thanks for any help

 

[TSny]

... but for finding J2, they took the area to be ∫2pir dr, which i think is the surface area along the inner cable.

∫2pir dr is actually the area of the end of the inner cable, $\pi$R₁², as you can see by carrying out the integral from 0 to R₁. The integral is summing the areas of concentric rings that fill up the entire area. This is necessary since the current density is different for each ring.