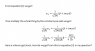PhysicsGirl90
- 17
- 0
Reading through my QM text, I came across this short piece on ladder operators that is giving me trouble (see picture). What I am struggling with is how to get to equations 2 and 3 from equation 1.
Can someone point me in the right direction? Where does the i infront of the x go?
Can someone point me in the right direction? Where does the i infront of the x go?