Hardy
- 11
- 1
I have been on an magnificent journey learning about the Tschirnhaus Transform and the Bring Radical. In summary, the transform takes any general 5th order polynomial:
##w^5 + A_ww^4 + B_ww^3 + C_ww^2 + D_ww + E_w##
into another polynomial of the form:
##x^5 + Dx + E##
The transform maps the roots of the general polynomial ( ## w_i ## ) into the roots of the transformed polynomial ( ## r_i ## ) using these set of equations:
## w_i = r_i^4 + ar_i^3 + br_i^2 + cr_i + d ##
The journey was so cool, cause I had to learn about and use elementary, power and symmetric polynomials. Additionally, and finally, solve some very complex equations . . . and I made it! . . . I think . . .
I am finding that if the original polynomial has all real roots, then I always find D and E are complex in the transformed polynomial. On rare occasions, I can find real D and E if the original polynomial has 3 real and 2 complex roots. I can always find real D and E if the original has 1 real and two pairs of complex roots. The question I pose hear is that can anyone confirm this is consistent with their understanding?
Finding the transform required first finding a, b, c and d and then computing D and E from them. In the all real case, D and E had to be complex cause it seems that the only way to complete the transform in the all real root case was such that a, b, c and d had to be complex (like a was the root of a quadratic that only had complex roots, for example).
To help demonstrate this is the case, if you look at the transform itself, you see that if ##r_i## is real, the ##w_i## has to be real. Its easy to see with one real root and the three real roots cases. But with 5 real roots, when a, b, c and d are complex, the real ##w_i## result in a quartic poly with complex coefficients (a, b, c and d), which always spit out the real roots! In other words, the basic transform seems successful on some level, but it not immediately intuitive.
To help, defining the Bring Radical as p in this equation:
##x^5 + px + 1##
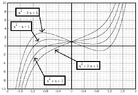
These series of plots demonstrate that only real p result in either 1 or 3 real roots, never 5. This would explain why p has to be complex in the all real case, since no real solution exist.

Similar plot result using ##x^5 + x + p## and ##x^5 + px + p##, except here, you only get 1 real root in the families of polys that result.
A second question that I came up with, is that it seems now that we are transforming a polynomial with rational coefficients to a polynomial that no longer has rational coefficients. Does this change and basic polynomial rules, specially in terms of the Galois fields that are spawned? I suspect that answer is no, you can't find surds of quintics (or higher) with closed equations, its just now, its true whether the coefficients are rational or irrational numbers.
Thanks for any input.
(PS - also thanks to fresh_42 for the Insight article on Galois theory and the inspiration to share here!)
##w^5 + A_ww^4 + B_ww^3 + C_ww^2 + D_ww + E_w##
into another polynomial of the form:
##x^5 + Dx + E##
The transform maps the roots of the general polynomial ( ## w_i ## ) into the roots of the transformed polynomial ( ## r_i ## ) using these set of equations:
## w_i = r_i^4 + ar_i^3 + br_i^2 + cr_i + d ##
The journey was so cool, cause I had to learn about and use elementary, power and symmetric polynomials. Additionally, and finally, solve some very complex equations . . . and I made it! . . . I think . . .
I am finding that if the original polynomial has all real roots, then I always find D and E are complex in the transformed polynomial. On rare occasions, I can find real D and E if the original polynomial has 3 real and 2 complex roots. I can always find real D and E if the original has 1 real and two pairs of complex roots. The question I pose hear is that can anyone confirm this is consistent with their understanding?
Finding the transform required first finding a, b, c and d and then computing D and E from them. In the all real case, D and E had to be complex cause it seems that the only way to complete the transform in the all real root case was such that a, b, c and d had to be complex (like a was the root of a quadratic that only had complex roots, for example).
To help demonstrate this is the case, if you look at the transform itself, you see that if ##r_i## is real, the ##w_i## has to be real. Its easy to see with one real root and the three real roots cases. But with 5 real roots, when a, b, c and d are complex, the real ##w_i## result in a quartic poly with complex coefficients (a, b, c and d), which always spit out the real roots! In other words, the basic transform seems successful on some level, but it not immediately intuitive.
To help, defining the Bring Radical as p in this equation:
##x^5 + px + 1##
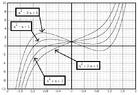
These series of plots demonstrate that only real p result in either 1 or 3 real roots, never 5. This would explain why p has to be complex in the all real case, since no real solution exist.
Similar plot result using ##x^5 + x + p## and ##x^5 + px + p##, except here, you only get 1 real root in the families of polys that result.
A second question that I came up with, is that it seems now that we are transforming a polynomial with rational coefficients to a polynomial that no longer has rational coefficients. Does this change and basic polynomial rules, specially in terms of the Galois fields that are spawned? I suspect that answer is no, you can't find surds of quintics (or higher) with closed equations, its just now, its true whether the coefficients are rational or irrational numbers.
Thanks for any input.
(PS - also thanks to fresh_42 for the Insight article on Galois theory and the inspiration to share here!)
Attachments
Last edited: