Racquetball's strange bouncing patterns

[KingNothing]

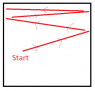
I play racquetball quite a bit as a hobby and competitively. One thing that I have noticed, and has baffled me for some time, is that on the sidewalls of a racquetball court, the ball's angle of incidence does not equal it's angle of reflection. It instead tends to (after repeated bounces) move at a normal to the wall.

See the diagram below. I am not talking about the ball hitting the floor at any given time, just the sidewalls. This is also at very fast speeds, I'm talking full-speed drive shots. Why does the ball do this? Certainly some of it is due to air resistance in the direction of the front wall, but that's got to be a small amount.

Could this be due to how the ball spins and distorts as it bounces off the sidewalls? If so, what equations govern this?

 

[Calrid]

Power and spin I expect has the greatest impact. Ever played pool or snooker?

The deviation from a mean will be in accordance with the angle of incidence and the angular momentum or the spin. The greater the spin the greater the deviation from mean. However this isn't that simple a calculation so just using the angular momentum and angle of incidence may well not give you an accurate indication, we'd also have to realize that the ball is a sphere and hence it won't always be incident at a fixed point. Where as I could easily show the equations for incidence and relation to spin, I'd find it quite hard to model this with accuracy given all the other factors taken into account.

In your diagram you'll probably find that left hand spin is applied narrowing the angle as it begins to lose momentum though the spin can in fact disappear or even in some circumstances become reversed. Again try playing pool note the reflective angle at pace, and at low speeds. They can be opposite depending if they strike a ball or how they impact with a straight object like the cushions. This due to other factors like top spin, back spin and the power of the shot and the time the ball hence spends sliding; also as noted above the exact angle of incidence and the way the balls shape is deviated more or less according to the power of the shot.

In pool it is easily possible for example to play a great deal of right hand spin and end up with the ball hitting the balk cushion with left hand spin instead or even reversing spin on a collision. This would be much easier to model with a pool ball where there is relatively little deformation of the ball than a raquetball.

 

[KingNothing]

Spin I expect. Ever played pool or snooker?

Yes, I play pool competitively as well. I am awesome at predicting these angles, but I'd like to know the equations governing them.

 

[Calrid]

Yes, I play pool competitively as well. I am awesome at predicting these angles, but I'd like to know the equations governing them.

Well the simple equations you can just google but for a complex picture I have no idea it's undergraduate calculus probably so I'll leave it to a mathmo to explain rather than giving simple equations that mean pretty much nothing.

 

[rcgldr]

The initial collision will be affected by whatever spin the racket put on the ball. After that, the ball now has spin that will reduce the angle of incidence on the next collision. Using your diagram, assume the ball has no spin when it hits the right wall. The ball will end up with clockwise spin and somewhat reduced angle of indicidence. Then the ball hit the left wall, and the spin is changed from clockwise to counter clockwise, reducing the angle futher still. The racket ball angular "elasticity" isn't very high so it ends up bouncing perpendicular to the wall.

If this were a ball with a high amount of angular elasticity, such as a superball, after hitting the second wall, the angle of incidence would be nearly zero, and it would end up nearly returning back to it's original position when struck by the racket. A more common experience with this is to bounce a super ball under a table, it hits the ground, then the bottom side of the table, then bounces back almost following the same path before hitting the underside of the table, returning to the thrower. Example videos:

 

[KingNothing]

I understand that this is due to spin. Can anyone point me to some equations that govern this?

 

[Calrid]

I understand that this is due to spin. Can anyone point me to some equations that govern this?

Actually bizarelly no. First time I tried google and all I get is mostly quantum issues which are nothing to do with classical systems.

I'm sure it's related to angular momentum but I can find no exact equation that relates mass to momentum and angular momentum and the index of incidence to angle. How strange? I have learned to utilise this by the basic skill of observation in games of skill. As to how it intrinsically works mathematically and according to a model though, I am not confident enough to moot a mathematical equation that models all x in t.

I understand this issue because I have spent a great deal of time playing pool and thinking about this, but I am sad to say I don't know the exact physics principles and nor it seems at face value does google, at least without trawling through thousands of hits.

 

[AIR&SPACE]

I actually just read a book talking about this: It's kind of a "tweener" book in that it presents the theories with a bit of math, but not very technical. Neat read.

"[URL Flight -- Dynamics of Frisbee's, Boomerangs, Samaras and skipping stones
by Ralph D. Lorenz[/URL]

If you want a more technical approach here are three of the sources he cites for the bouncing ball section. You may or may not be able to view these based on copyright permissions.
"[URL of the horizontal coefficient of restitution for a superball
and a tennis ball
Rod Cross[/URL]


Happy reading!
The way balls bounce
N James Bridge

"[URL bounce of a ball
Rod Cross[/URL]

 

[Curl]

I understand that this is due to spin. Can anyone point me to some equations that govern this?

yes, use Newton's laws, they always work for classical mechanics.