- #1
bolzano95
- 89
- 7
Just started learning about uniform circular motion. I really don't understand how we get aΔt2/2 on the side. I also searched on the internet for a similar derivation, but there are none so simple.
Thanks for your help!
P.S There is a mistake in calculation in second line (textbook error).
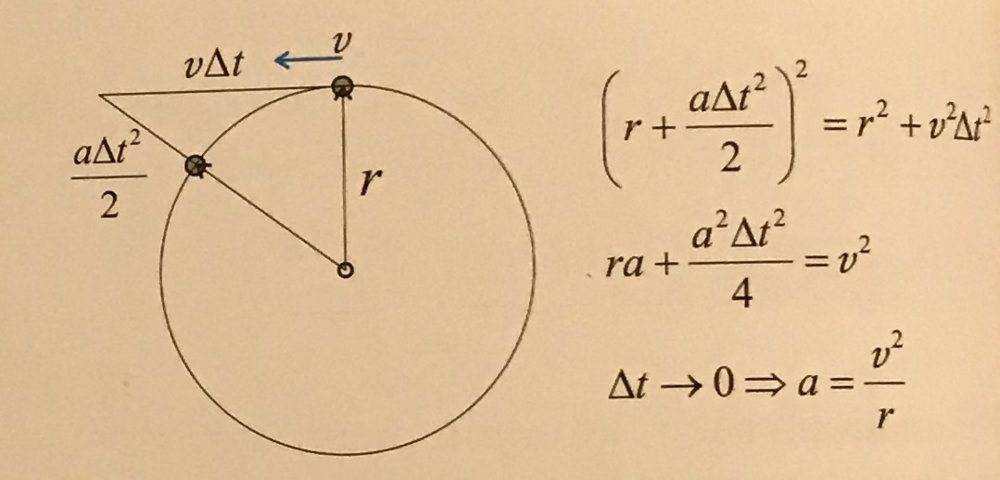
Thanks for your help!
P.S There is a mistake in calculation in second line (textbook error).