SUMMARY
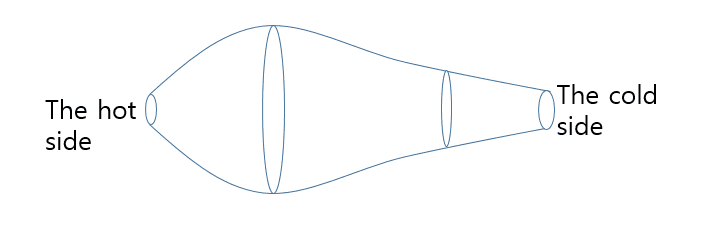
The discussion focuses on calculating the rate of conduction heat transfer (Q) when the hot side and cold side areas differ. It emphasizes that thermal conductivity is a material property, while conductance or resistance must be considered when areas vary. The equation $$Q=kA(x)\frac{dT}{dx}$$ is introduced for cases with gradually changing cross-sectional areas, leading to $$Q=k\frac{\Delta T}{\int_0^L{\frac{dx}{A(x)}}}$$ for more complex geometries. The need for assumptions regarding uniformity and directionality of heat flow is also highlighted.
PREREQUISITES
- Understanding of thermal conductivity and its properties
- Knowledge of heat flux and its dependence on cross-sectional area
- Familiarity with the heat conduction equation
- Basic calculus for integrating variable cross-sectional areas
NEXT STEPS
- Study the derivation and application of the heat conduction equation in different geometries
- Learn about the differences between thermal conductivity, conductance, and resistance
- Explore numerical methods for solving 2D and 3D heat conduction problems
- Investigate practical applications of heat transfer in engineering contexts
USEFUL FOR
Students and professionals in physics, engineering, and materials science who are interested in heat transfer principles and their applications in real-world scenarios.