roam
- 1,265
- 12
- TL;DR
- I am trying to generate ##M## random numbers which are exponentially distributed and whose sum adds up to ##N##. However, the re-scaling always causes the numbers to become uniformly distributed.
For simplicity, let ##N=1##. The following histograms show my results. The generated random numbers are initially exponentially distributed. But after re-scaling they become almost uniformly distributed.
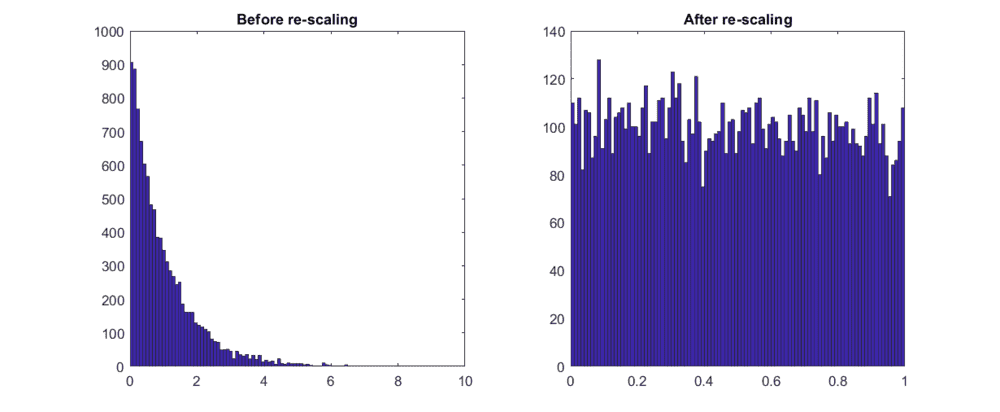
What is the cause of that, and is there a solution?
P.S. Here is my code in Matlab:
What is the cause of that, and is there a solution?
P.S. Here is my code in Matlab:
Matlab:
subplot(121)
samples = 10000;
lambda = 1;
X = -log(rand(samples,2))/lambda;
hist(X(:,1),100)
subplot(122)
X = X./sum(X,2); % re-scaling
hist(X(:,1),100)