Realistic steering wheel angle when car follows points along a path

[Guitz]

TL;DR

I'm developping a traffic simulation on Unreal Engine

Good morning ,

I managed to simplify the physics of my car with only the centrifugal and traction forces. If I'm in control of it, the realism is acceptable for a city builder. On the other hand, I encounter a problem when the car follows an array of points.

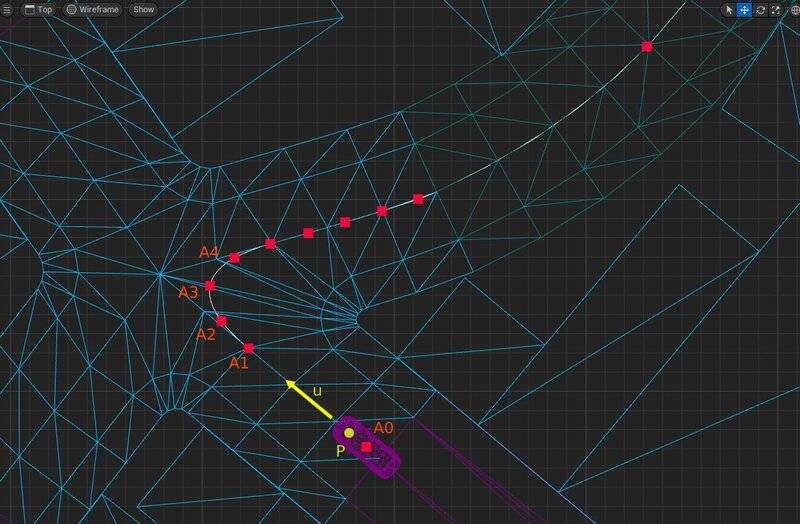
The path of the car on my graph consists of an array of position vectors A[],
I'd like the steering wheel to rotate realistically based on the car's position and rotation relative to each A .
The unit vector u is always in the same direction as the front of the car, P is located between the 2 front wheels.

The problem with my algorithm is that on certain portions, the car tends to zigzag.

Any idea please to remove this zigzag effect?

 

[A.T.]

Any idea please to remove this zigzag effect?

Start by finding out what is causing it.

Do you want the car to follow the path and the steering is for the realistic look only? Then you should control the motion by the path, not by forces. Derive the steering for visuals from the motion of the wheel locations relative to the ground.

 

[Baluncore]

Any idea please to remove this zigzag effect?

The steering wheel angular position will track the radius of curvature of the track on the ground. You show the points approximated by a smooth curve. Compute the RofC of that line, then move the steering wheel to track that, as the vehicle moves along that line.

 

[Guitz]

Sorry i forgot to show you the algorithm :

Every frame if CarIsMoving = true :
If DegreesAngle(A[i] – P, u) >= 90
we go to next A[i], so
      i = i+1
 Else,
 
DeltaSteeringAngle = DegreesAngle(RotateVectorAroundZAxis(u, SteeringAngle), A[i] – P)/15
SteeringAngle = SteeringAngle + DeltaSteeringAngle

 

[Baluncore]

Does DegreesAngle(A – P, u) range from -180° to +180°, or from 0° to 360° ?

I would expect; ABSolute ( DegreesAngle(A – P, u) ) >= 90
or; DegreesAngle(A – P, u) >= 180

I think you will need a Bézier curve approximation to the sparse waypoints to determine the steering wheel angle.

 

[Guitz]

Does DegreesAngle(A – P, u) range from -180° to +180°, or from 0° to 360° ?

I would expect; ABSolute ( DegreesAngle(A – P, u) ) >= 90
or; DegreesAngle(A – P, u) >= 180

I think you will need a Bézier curve approximation to the sparse waypoints to determine the steering wheel angle.

Yes i used Abs() but i wanted to simplify the algorithm to make it easier to read on forums

 

[Baluncore]

Yes i used Abs() but i wanted to simplify the algorithm to make it easier to read on forums

We can only look for problems in the code you post.
How does the car navigate between the waypoints ?
How could a car do a three-point-turn ?

 

[Guitz]

How does the car navigate between the waypoints ?

I update the Thottle property everyframe, but car speed is bounded by every A[].SpeedLimit. In fact
A[] is a PathData struct array storing Location, Tangent, SpeedLimit properties

 

[Baluncore]

You show a curved path, but only use waypoints on that curve.
Do you know what you mean by tangent? I don't.

 

[Guitz]

You show a curved path, but only use waypoints on that curve.
Do you know what you mean by tangent? I don't.

these tangents are simply tangents on every waypoint. I use them to correctly orientate the car in the correct direction when i spawn it at a specific A[0]

 

[Baluncore]

If you have two points with tangents, then they define a circular arc. The vehicle orientation can change as it moves in single frame steps along that arc, and the steering wheel position can be determined by the radius of curvature of the arc.

 

[Guitz]

If you have two points with tangents, then they define a circular arc. The vehicle orientation can change as it moves in single frame steps along that arc, and the steering wheel position can be determined by the radius of curvature of the arc.

Thank you so much, ill try this approach

 

[Baluncore]

If you use a circular arc, the steering will jump when you reach a waypoint on a curve, because the radius changes instantly. If you use a parabolic curve between the two tangents, it will not have a step change, but the steering wheel will oscillate a little either side.
The next refinement beyond a parabolic curve is a spline, or a Bézier curve. Then, while travelling a segment, you always consider four points, the two points behind and the two points ahead.

 

[Baluncore]

Car steering wheel.
https://cs.stackexchange.com/questi...ulate-the-maximum-curvature-of-a-cubic-spline

https://en.wikipedia.org/wiki/Bézier_curve
https://en.wikipedia.org/wiki/Curvature#Local_expressions

 

[Guitz]

Start by finding out what is causing it.

Do you want the car to follow the path and the steering is for the realistic look only? Then you should control the motion by the path, not by forces. Derive the steering for visuals from the motion of the wheel locations relative to the ground.

Hi A.T.,

if the car follows a path without taking into account the forces, it is the most optimized (i need to spawn 5000 vehicles in my city builder) but is there a way to make it realistic enough?

As I said, I take into account the centrifugal force and the traction force only,
but i am open to your suggestion.

 

[Guitz]

please guys, have a look at 2:25



The developer has the same zigzag problem as me.
This is a very complicated issue to solve also considering i must also optimize/simplify a lot because i will allow the user to spawn max 5000 vehicules at runtime.

Thanks for your help

 

[A.T.]

if the car follows a path without taking into account the forces, it is the most optimized (i need to spawn 5000 vehicles in my city builder)

Then do it without forces:
- Place the center of the back axle on the path at some point P and rotate the car such that the back axle is perpendicular to the path at P.
- Orient the front wheel axles, so they point to the center of curvature of the path at P. Note that for a straight path the center of curvature is at infinity, so you might need a threshold to deal with that numerically.

https://en.wikipedia.org/wiki/Ackermann_steering_geometry

https://en.wikipedia.org/wiki/Osculating_circle

but is there a way to make it realistic enough?

What is "realistic enough"? Use the most efficient approach, then check how it looks, and improve only if needed.

The developer has the same zigzag problem as me.

If you try to follow an exact path using steering inputs, forces and Newton's Laws, you have a control problem, which might not be worth the trouble, if it is only for visuals:
https://en.wikipedia.org/wiki/PID_controller

 

[Baluncore]

You know the direction of the track at the front of the car. Point the front wheels in that direction. The rear wheels will follow in a pursuit curve, so always aim the back wheels at the front wheels. The car body will be oriented the same way as the rear wheels.

 

[Guitz]

Thanks again, i'll try to implement this

 

[Guitz]

Hello everyone,

As suggested i will have to use osculating circles:



What do you think is the best optimization/realism compromise?

Should the car's OsculatingCircle be updated every frame from its trajectory spline? Or is it realistic enough to bake 1 OsculatingCircle per checkpoint, and interpolate car position / front wheels rotation / car rotation between them?

 

[A.T.]

What do you think is the best optimization/realism compromise?

Try it and compare. Computing the circle approximation from 3 points on the path should not be that computationally expensive. Or there might be an analytical formula for the type of spline you are using.

 

[Guitz]

Hi all, finally i computed osculating circle every frame.
Thank you very much for giving me this solution. Not only this method offers a clean car behavior, but also it is more optimized than using Newton's 2nd Law by following a array of points.