Receiver Circuit Question -- What role does this antenna capacitor play?

[Baluncore]

It's for tuning the antenna to its resonance.

Then can you explain why the capacitor is not adjustable, it is fixed in value, yet it works with any antenna connected.

 

[tech99]

It is true that some antennas can be brought to resonance with a series capacitor, which effectively shortens the electrical length, but in this case it is not the purpose of the capacitor. It is undesirable to have a resonant antenna with a regerative detector, because it causes large variations in the amount of feedback required as the tuning is varied. It can even result in complete suck-out frequencies where oscillation cannot be obtained.

 

[The Tortoise-Man]

It's for tuning the antenna to its resonance.

But for the tuning in the linked circuit there is the LC-tank (ie coil L_1 + cap 10-140 pf)
responsible, or not? Or do you mean that the intention for adding of this coupling
capacitor 2-18 pf a just a jazzing up the tuning part of the circuit? So not really
neccessary, but makes it more powerful? Nothing more?

 

[tech99]

The capacitor is essential because without it the tuned circuit is heavily damped by the antenna and oscillation cannot be obtained.

 

[Baluncore]

The key parameter is the ratio of the antenna coupling capacitor to the tuning capacitor. That ratio decides (in part) the proportion of the resonant current that is diverted from the tuned circuit to the antenna, and so the Q of the tuned circuit.

If a variable capacitor is used to tune the resonant circuit, then the Q will change over the band as the tuning capacitor changes.

In effect, the changing voltage of the tuned circuit, pumps current through the two capacitors in proportion to their capacitance values. C = Q / V ; Q = I·t ; ∴ i = C · dv/dt.

Because the antenna impedance is in series with the antenna coupling capacitor, the antenna impedance may reduce the proportion of current lost to the antenna, and so increase the Q of the tuned circuit.

 

[The Tortoise-Man]

The key parameter is the ratio of the antenna coupling capacitor to the tuning capacitor. That ratio decides (in part) the proportion of the resonant current that is diverted from the tuned circuit to the antenna, and so the Q of the tuned circuit.

Maybe here is a reason for my confusion:
You are talking about the "Q of the tuned circuit".
Firstly, what do precisely mean by
the "tuned circuit" in the image from
https://www.frostburg.edu/personal/latta/ee/twinplex/schematic/twinplexschematic.html?

I thought that the part of this receiver which is called
the "tuned circuit" is only the LC-tank given
by the parallel L_1 and capacitor with 10-140 pf below on the
right?

If my last statement is true, then I not understand
why as you said the Q of the tuned circuit (this LC-tank)
depends also on the coupling capacitor.

Indeed, the Q of a parallel LC-unit has a concrete formula
(see https://en.wikipedia.org/wiki/Q_factor#RLC_circuits);
note that of course the formula requires that the
LC-tank should also have a resistor; I guess that
in the linked image it is implicitely assumed to be there
(eg real coil has always a additional real resistance) but not
explicitely drawn).

And due to this formula it seems that according to it there
is no dependence of the tuned circuit's Q to the coupling capacitor.

So what do you mean by that the ration of the
antenna coupling capacitor to the tuning capacitor
(clearly it depends on the coupling capacitor)
decides (indirectly) the Q of the tuned circuit?

Maybe when we are talking about "tuned circuit" we are thinking
of different parts of the total unit? What is the
"tuned circuit" for you there?

 

[Baluncore]

If my last statement is true, then I not understand why as you said the Q of the tuned circuit (this LC-tank) depends also on the coupling capacitor.

Because the resonant LC tuned circuit has many different ways to lose energy, and the most significant one of those is to the antenna, via the coupling capacitor. Another is the resistance of the L and C components, then there is eddy current loss in the nearby chassis from the inductor's magnetic field, and some radiation from the inductor. A small amount of energy goes to drive the VT grid. In the real world, Q is not just the simple LCR textbook equation, it is one corner of the universe.

There are also two sources of energy that maintain the LC resonance. One is the signal from the antenna, the other is the regenerative feedback that makes up for many of the losses.

 

[The Tortoise-Man]

Because the resonant LC tuned circuit has many different ways to lose energy, and the most significant one of those is to the antenna, via the coupling capacitor. Another is the resistance of the L and C components, then there is eddy current loss in the nearby chassis from the inductor's magnetic field, and some radiation from the inductor. A small amount of energy goes to drive the VT grid. In the real world, Q is not just the simple LCR textbook equation, it is one corner of the universe.

There are also two sources of energy that maintain the LC resonance. One is the signal from the antenna, the other is the regenerative feedback that makes up for many of the losses.

Interesting. So what you mean is that the Q factor
of the tuned circuit considered as the red encircled
thing in image below highly depends on what stuff is in the
magic box on the left, right?

But finally what about this quoted formula from
https://en.wikipedia.org/wiki/Q_factor#RLC_circuits
which suggests that the Q of parallel LC-tank depends
only on components L, C, R? So it's finally just
a poor's man approximation tool for some special
cases? Or, let me say, under
which assumptions on the total network this formula
gives "nearly" the correct Q of the LC-tank?

 

[Baluncore]

Your irrational line breaks make it hard to understand your reasoning.

If the only losses were the series resistance of the inductor, or the dielectric losses of the capacitor, then the wikipedia simplicity would be correct.

But in the real world there are other networks in parallel with L and C that lower the Q. There is no advantage in having an isolated tuned circuit if it does not have energy inputs and energy outputs.

 

[DaveE]

Interesting. So what you mean is that the Q factor
of the tuned circuit considered as the red encircled
thing in image below highly depends on what stuff is in the
magic box on the left, right?

View attachment 292703

But finally what about this quoted formula from
https://en.wikipedia.org/wiki/Q_factor#RLC_circuits
which suggests that the Q of parallel LC-tank depends
only on components L, C, R? So it's finally just
a poor's man approximation tool for some special
cases? Or, let me say, under
which assumptions on the total network this formula
gives "nearly" the correct Q of the LC-tank?

Personally, I don't see much value in dealing with the Q of a resonator if you haven't included all of the loss elements. I suppose you could; it's all just definitions, I guess. But I would be careful about drawing arbitrary boundaries. The way the tank works depends on all of the "stuff", not just what's nearby in the schematic.

 

[The Tortoise-Man]

Your irrational line breaks make it hard to understand your reasoning.

If the only losses were the series resistance of the inductor, or the dielectric losses of the capacitor, then the wikipedia simplicity would be correct.

But in the real world there are other networks in parallel with L and C that lower the Q. There is no advantage in having an isolated tuned circuit if it does not have energy inputs and energy outputs.

Ok, maybe I understand your point and the reason for my confusion now (correct
me if I'm wrong):

Seemingly we talked past each other on the point what the considered "tuned circuit" should be.
So I guess that you implicitely considered the antenna impedance + the coupling capacitor
as part of it, while I (wrongly?) assumed that when you talked about "tuned circuit" you literally
only mean this LC-thing. In pictures:

Well, if you indeed meant by "tuned circuit" the blue encircled thing, then clearly it's Q depends on the coupling capacitor (I conjecture that you meant exactly this thing because as you said the Q of it should depend on antenna losses, while the Q of the green encircled thing has - as wiki formula says - no dependence on the antenna components & coupling capacitor. Did understood your point now correctly?

 

[Baluncore]

Seemingly we talked past each other on the point what the considered "tuned circuit" should be.
So I guess that you implicitely considered the antenna impedance + the coupling capacitor
as part of it, while I (wrongly?) assumed that when you talked about "tuned circuit" you literally
only mean this LC-thing.

No.
You cannot draw lines sensibly about components that are connected with wires, because signals travel both ways on the wires and the lines cannot form secure bulkheads.

The tuned circuit is the LC resonant circuit, where energy is circulated between L and C. That may have internal losses that set the maximum Q.

The tuned circuit is also externally loaded.
The external resistive loads further reduce the Q of the tuned circuit.
The external reactive loads change the frequency of the tuned circuit.

 

[Tom.G]

Ok, maybe I understand your point and the reason for my confusion now (correct
me if I'm wrong):

Seemingly we talked past each other on the point what the considered "tuned circuit" should be.
So I guess that you implicitely considered the antenna impedance + the coupling capacitor
as part of it, while I (wrongly?) assumed that when you talked about "tuned circuit" you literally
only mean this LC-thing. In pictures:
View attachment 292775

Well, if you indeed meant by "tuned circuit" the blue encircled thing, then clearly it's Q depends on the coupling capacitor (I conjecture that you meant exactly this thing because as you said the Q of it should depend on antenna losses, while the Q of the green encircled thing has - as wiki formula says - no dependence on the antenna components & coupling capacitor. Did understood your point now correctly?

For what it is worth @The Tortoise-Man, I agree with your above statement. My reading of this thread brought me to the same conclusion you reached.

Cheers,
Tom

 

[The Tortoise-Man]

No.
You cannot draw lines sensibly about components that are connected with wires, because signals travel both ways on the wires and the lines cannot form secure bulkheads.

The tuned circuit is the LC resonant circuit, where energy is circulated between L and C. That may have internal losses that set the maximum Q.

The tuned circuit is also externally loaded.
The external resistive loads further reduce the Q of the tuned circuit.
The external reactive loads change the frequency of the tuned circuit.

I'm confused. Maybe I just too stupid and too wikipediazed to understand your interpretation of Q. I thought that it's always possible in an arbitrary circuit to associate to every bunch of neighboured components a Q, which depends only of the parameters of these components and not external components,

eg that in following simple circuit we can associate a factor Q-factor $Q_{L1C1R1}$ to L1-C1-R1-unit only, but also eg a $Q_{L2R2}$ to L2-R_L-only only, even to any individual reactive component(https://en.wikipedia.org/wiki/Q_factor#Individual_reactive_components),
like C2 alone, if we realize that real C2 has a small real restance. Of course we can associate a Q to the total circuit. The point I want lake to emphasize is Q's modularite I assumed.

And I thought that this Q always depends only on the components to which it is associated, not the external one. But you said that's not the case, so it depends on external components, and I have to admit that sound like a culture shock to me, nevertheless I would like to understand your point better.

If it's ok for you, could we go one step back? What is your precise definition of Q? And assume we have an example circuit like the above, consider it as a kind of "playground". According to your definition
of Q, to which components or sub parts of this circuit you can associate a Q?

How do you calculate it? As far as I understand you correctly, you not get the formulas I found in wikipedia. Could you give an example calculation of some component of this circuit? Or could you give a reference where the Q is discussed in the way you explained it? Ie that it depends also on external components?

 

[Baluncore]

I thought that it's always possible in an arbitrary circuit to associate to every bunch of neighboured components a Q, which depends only of the parameters of these components and not external components,

Find an "energy flywheel" such as a resonant LC circuit with some R. As an isolated circuit it will have a Q. That is the extent of the wikipedia analysis. That Q is a maximum for the greater circuit.

Then study all the ways the resonator can lose energy to the surrounding environment. How will the choice of external components change the rate of energy loss? Those external loads will lower the Q of the greater circuit to below the wikipedia calculated maximum.

In this case a larger coupling capacitor would increase the losses through the anttenna, so it would reduce the Q of the greater circuit.

 

[The Tortoise-Man]

Then study all the ways the resonator can lose energy to the surrounding environment. How will the choice of external components change the rate of energy loss? Those external loads will lower the Q of the greater circuit to below the wikipedia calculated maximum.

In this case a larger coupling capacitor would increase the losses through the anttenna, so it would reduce the Q of the greater circuit.

Ok, I think I understand your point. So if we want to study the Q factor of a LC-circuit in the sense you thinking about it, one can rephrase to idea as follows on following elementary example:

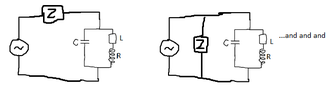
Say as an example we want to analyse the function Q of a elementary parallel
LCR circuit in the sense you think about is:

Then this Q is a function of the three components $L, C, R$ components and the impedance
$Z_E=R_E+jX_E$ of an abstract environment component which we can attach to the "scaffold of
the total circuit"

in any feasible way we want, like eg

ie any configuration how can we attach a or more environment component(s) to this scaffold of
the circuit is allowed.

How to calculate this $Q (=Q(L, C, R; Z_E))$ for a
given environment component with impedance $Z_E$?

We calculate the $Q(L, C, R; Z_E)$ just as the Q of the TOTAL circuit, ie with the LC-circuit and
the environment component by the techniques from wikipedia/ "stadard textbook methods" how to calculate the Q faction of a fixed circuit.

Eg if the environment compoent is a capacitor parallel to the the LCR-circuit the Q(L, C, R; Z_E) equals to the Q of the total circuit:

Finally, we observe that the "wikipedia/textbook" Q of the LC-circuit consides with the case when
there is no environment compoent, ie Q= Q(C, L, R; -):

Did I understood your idea of the Q factor now correctly?

 

[DaveE]

Say as an example we want to analyse the function Q of a elementary parallel
LCR circuit in the sense you think about is:

That's a series resonance. Sorry for nit-picking though. In a series configuration low loss requires low resistance. In a parallel configuration low loss requires high resistance.

Did I understood your idea of the Q factor now correctly?

Yes, I think you've got it. More complex networks can get confusing though and people will either disagree or be sloppy about what Q is. In those cases, I prefer the basic physics approach, where Q is simply an expression of the energy loss that the reactive resonant elements experience. Of course, while the concept is simple, the calculations aren't always. The biggest confusion arises when a network has more than one resonance. I claim each resonance has its own Q (a more mathematical approach), others disagree and will assign a more global definition; one Q for everything (a more functional approach). We are both right, in the proper context. So, for more complex networks, you'll just have to explain the version you are using, I think.

 

[Tom.G]

Say as an example we want to analyse the function Q of a elementary parallel
LCR circuit in the sense you think about is:

That's a series resonance.

I'm curious @DaveE, if that is a series resonant circuit, could you please show us/draw a parallel resonate circuit?

Thanks.

 

[Baluncore]

Ok, I think I understand your point.

Your symbol for a zero impedance AC voltage source, that short circuits the tuned circuit confuses things. For this analysis, I simply assume there will be one unit of energy circulating in the tuned circuit at the start of the analysis.

The antenna is a load impedance, Z_ant.
If you later need a signal from the antenna to model the gain of the circuit, insert a voltage source, V_ant in series with the antenna Z_ant. But that signal source is not needed to understand or model the resonant circuit.

 

[DaveE]

The mathematical version of Q goes like this:

That quadratic term in the impedance can be expressed in a canonical form of $(1+\frac{1}{Q}(\frac{s}{\omega_o})+(\frac{s}{\omega_o})^2)$

Then, you will find that $\omega_o = \frac{1}{\sqrt{LC}}$, $Z_o = \sqrt{\frac{L}{C}}$ (the characteristic impedance).

For the series resonator, $Q = \frac{Z_o}{R}$

For the parallel resonator, $Q = \frac{R}{Z_o}$

These circuits and canonical forms are worth memorizing, IMO. You'll see it in electronics, mechanics, acoustics... everywhere. It is the solution to the simple harmonic oscillator with losses.

Each pole or zero in the transfer function (impedance, gain, whatever...) will either be a single Real value, or it will be a quadratic pair. Those quadratic pairs of roots (or zeros) are each Complex and can be characterized by their frequency ($\omega_o$) and their Q.

However, while all of this is true, it is also a particular analytical method that is favored by some and not by others. If you study control systems, filter design, etc. then this is how you think. If you study how to actually build radios like people in the 1930's then you speak in different terms about the same concepts.

 

[DaveE]

that signal source is not needed to understand or model the resonant circuit.

Yes, this is an important concept. A bell is a resonant structure whether you ring it or not. The resonance is all about what happens after you've put some energy in, not so much about where the stimulus came from.

 

[The Tortoise-Man]

Ok, so it's a matter of nomenclature. If we replace 'parallel LCR circuit' everywhere I wrote it by 'series circuit' as Dave in #77 suggested.

And furthermore if we remove everywhere in my images in #76 the AC voltage source ~ as
Baluncore suggested and instead think of it that in all circuits I draw there is a fixed one unit of energy circulating:

Is then what I wrote about my attempt to understand Baluncore's
interpretation of Q factor after making correction on these two points in
post #76 correct?

 

[Baluncore]

Correct.

 

[The Tortoise-Man]

By the way: recently there came another simple idea into my mind how maybe role of red tagged capacitor ('the coupling capacitor') from my post #1 (which was my initial problem with this circuit) might be understood in more simple terms if someone is not completely familiar with this stuff around "Q factor" or feels at least uncomfortable in it as follows:

namely, is it correct that the part

as a whole may be recognized as a bandpass filter, and the indispensability of the coupling capacitor here is expressed in the fact that without it the blue encircled part simply would not be a bandpass filter any more. So the coupling capacitor is necessary to complete it's functionality as a bandpass filter.

Is this interpretation of the role of the coupling cap also correct? Or does it here missing the point?

(indeed I pondered a while why if the blue encircled unit is indeed a bandpass filter there are two capacitors C2 and C3 in the tank used. My conjecture: the reason why they coexist there might be that the receiver circuit above is designed to receive frequencies from two disjoint bands. If the desired frequence lies in one band, C2 is used to tune it, if on the other, then C3 does the job; is this interpretation correct?)

 

[Averagesupernova]

Look up the definition of bandspread and bandset it will likely answer your question.

 

[The Tortoise-Man]

Look up the definition of bandspread and bandset it will likely answer your question.

Ok, this answers why the tank in #84 could have two capacitors C2 and C3, right? So essentially that allows a qualitatively more advanced control over tuning the desired frequence?

Ok, what about my 'attept' to interpret the red encircled coupling capacitor as functional part of the blue encircled unit: Is the only job of this blue unit indeed the bandpass filtering and is then as I conjectured the job of the coupling cap just to coplete it (since otherwise it would not be a bandpass filter)?

 

[Averagesupernova]

Think of it this way: Anything you attach to a tank circuit will lower the Q. Being able to adjust the amount of coupling will affect this.

 

[Baluncore]

So the coupling capacitor is necessary to complete it's functionality as a bandpass filter.
Is this interpretation of the role of the coupling cap also correct? Or does it here missing the point?

There is no bandpass filter, only the tuned circuit. You are missing the point.
The Q of the front end is roughly; Q = (C2+C3) / C1.
That is because AC current is shared in proportion to capacitance; i ∝ C · dV/dt .
For a fixed C1, as you tune across the band, (C2+C3) changes, so the Q must also change.
C1 allows you to adjust the Q and the degree of antenna coupling to the signals of interest.

 

[The Tortoise-Man]

There is no bandpass filter, only the tuned circuit. You are missing the point.
The Q of the front end is roughly; Q = (C2+C3) / C1.
That is because AC current is shared in proportion to capacitance; i ∝ C · dV/dt .
For a fixed C1, as you tune across the band, (C2+C3) changes, so the Q must also change.
C1 allows you to adjust the Q and the degree of antenna coupling to the signals of interest.

I'm not completely convinced. For our considerations about the issue 'Is it
a bandpass filter or not' we can drop the third capacitor C3 (as Averagesupernova
noted the precence of two capacitors C2 and C3 has only to do with bandspread issues;
let's forget it in next considerations) and consider the simplified version of right picture
in #84:

Then as you said it's Q is proportional to C2/C1, right? If the C1 and C2 a variable like
in case of our circuit on the left in #84, isn't the unit in the picture above
nothing but a possible design of "variable" bandpass filter is the sense that if we fix some C1 and C2 it would become a "usual" bandpass filter?

The reason why I think so is that essentially that's what a bandpass filter should do, to let passing signals of desired frequence and block the others deviating from the resonance frequence. And it's "sharpness" on doing that is quanified by the Q factor, right?

Or is your statement that this circuit by construction cannot be a bandpass filter (because eg maybe there is something missing?)

 

[Baluncore]

Or is your statement that this circuit by construction cannot be a bandpass filter (because eg maybe there is something missing?)

Without an input there is no point having a receiver.
The energy input from the antenna can be coupled into the tuned circuit by a tap on the inductor, or by a small value capacitor. The tuned circuit is required no matter which way it is done. The coupling capacitor does not provide an additional band-pass feature to the circuit.

A band-pass filter is distinct from a tuned circuit in that the BPF has steep sides with a flatter top. Stagger tuned circuits can be lightly coupled to make a BPF. But here there is only one tuned circuit.

If you were to model the antenna as a tuned circuit, then couple it through C1 to the L//C2 tuned circuit, you might claim it becomes a BPF. But the antenna for MW is under-size, so is a wider-band structure, not a tuned circuit by itself.