B Reduced mass to atomic mass units conversion help please

[TheCelt]

Hello

I am trying to understand how to write the reduced mass into atomic mass units but i am confused how it was done.

The equation is

$$m_1m_2/(m_1+m_2)$$

For two similar masses in my particular case i have:

$$m^2 / 2m = 1/2 * m$$

Then to convert to atomic mass units, the book says it gives:

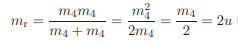
But how did they get that value? I had $$1/2 * u$$My conversion must be failing me, i am not sure how they got that value..

 

[BvU]

So the book has $m_4 = 4u$ while you have $m_4 = u$ ?

Hard to tell which is which on PF since $m_4$ hasn't been introduced here. Is it described somehow in the book ?

 

[TheCelt]

@BvU it was representing a $$_2^4 He$$

Don't know how to write it inline with my sentence, anyway it does seem I forgot that it would be 4u.

 

[BvU]

All clear ! (the subscript 4 was a giveaway )

Inline $\LaTeX$ by enclosing it in double #: $\LaTeX$