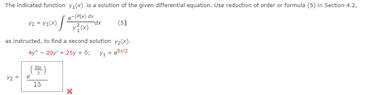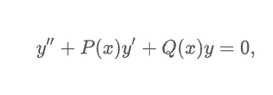SUMMARY
The discussion centers on the reduction of order problem for second order linear differential equations. The participant identified an error in their approach by failing to convert the equation into standard form. By dividing the equation by 4, they successfully derived the correct solution. This highlights the importance of proper equation formatting in solving differential equations.
PREREQUISITES
- Understanding of second order linear differential equations
- Familiarity with standard form of differential equations
- Basic algebraic manipulation skills
- Knowledge of reduction of order technique
NEXT STEPS
- Study the standard form of second order linear differential equations
- Practice the reduction of order method with various examples
- Explore the implications of equation manipulation on solution accuracy
- Review common mistakes in solving differential equations
USEFUL FOR
Students and educators in mathematics, particularly those studying differential equations, as well as anyone involved in mathematical problem-solving and analysis.