Reflection and refraction of light problem

[bbangel615]

Homework Statement

3. Assume the slab is perfectly rectangular and has width W.
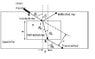
(a) Calculate the distance (L) the light travels INSIDE the block as a function of W and the angle t1.
(b) From the right-angled triangle with vertices IPE calculate the lateral displacement x in terms of the incident and reflected angles and the width of the sample.
(c) If the incident angle is 60 degree, n=1.81, and W= 8.0 cm, what is x?

4.)

Homework Equations

They mentioned Snell's law and how transmitted ray is parallel to the incident ray. n1sin(O1)=n2sing(02) 0=delta or whatever the circle with a little curve on the top is called. a diagram is attached.

The Attempt at a Solution

I really don't get this. help:(

 

[Poop-Loops]

The picture is really poor quality, but let's see if I deciphered it correctly.

So I'm assuming L is the length of the Refracted wave and that's what you want to find based on the width W and angle you shine the laser at, right?

So Let's take the two extreme cases. You shine the light right into the slab at a normal interface, so it's not at an angle at all. Based on that picture, you can see that the laser will go straight through the slab and come out the other side, right? Now if you lay the slab flat and shine the laser across it, it will just skim the surface and really never come out the other side, right? Basically you get "infinity".

Well, how do you get infinities? By dividing by a number that gets closer and closer to zero, right? That's pretty much the only real way of getting it.

So... you have a number W and dividing it by something can give you either W back at 0 degrees or infinity at 90 degrees. Do you know of a function that is 1 at 0 degrees and 0 at 90 degrees?

 

[alphysicist]

Hi Poop-Loops,

The picture is really poor quality, but let's see if I deciphered it correctly.

So I'm assuming L is the length of the Refracted wave and that's what you want to find based on the width W and angle you shine the laser at, right?

So Let's take the two extreme cases. You shine the light right into the slab at a normal interface, so it's not at an angle at all. Based on that picture, you can see that the laser will go straight through the slab and come out the other side, right? Now if you lay the slab flat and shine the laser across it, it will just skim the surface and really never come out the other side, right? Basically you get "infinity".

No, I don't think that's right. If the incident ray is right at 90 degrees to the normal, the ray that refracts in will be less than 90 degrees; in fact it will be at the critical angle for that material in air. The length of the refracted ray inside will be finite.

I think a good approach here for part a would be to construct a triangle with the length L as one of the sides.