Refraction through different mediums: calculating multiple angles help

[lpettigrew]

Homework Statement

Hello, I have a question concerning calculating the angles of refraction through different mediums. I have attached the questions and a photograph of my workings. I have answered the question fully and thoroughly shown my method but I would be extremely grateful if someone was able to review all of my workings to see if the angles I have calculated are correct. I have not faced such a broad refraction calculation problem like this before which is why I feel a little unsteady.
The question states ;
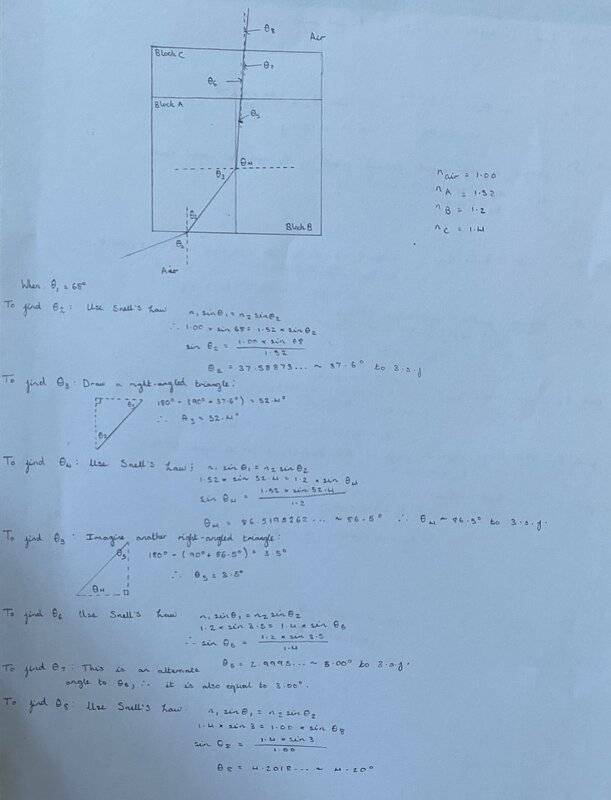
The image attached depicts three different mediums joined together. Block A has a refractive index of 1.52
Block B has a refractive index of 1.2
Block C has a refractive index of 1.4.
A ray of light travels through air into Block A, (assume air has a refractive index of 1.00).

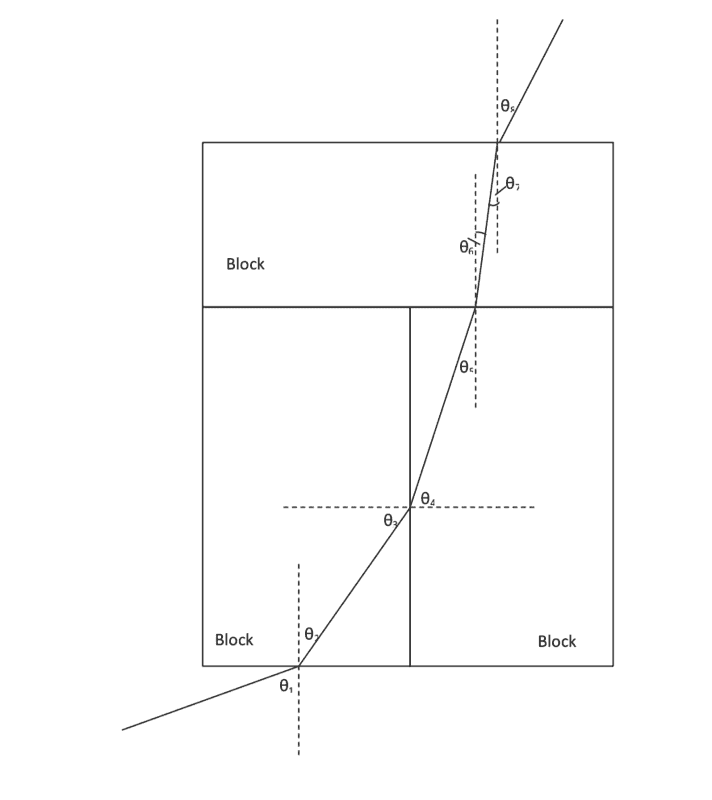
1. The diagram displays the path of light when θ1 = 78.
Calculate all of the remaining angles up to and including the point where it leaves the blocks (θ2 to θ8).

2. Draw another diagram where the angle of incidence of θ1 = 68°. Calculate all of the angles up to and including the point where it leaves the blocks.

Relevant Equations

Snell's Law; n1sinθ1=n2sinθ2

1. I have calculated the first angle using Snell's Law and with subsequent proceeding angles I am uncertain whether my workings are correct since I have used basic laws of geometry that all internal angles of a triangle add up to 180 degrees and that alternate angles are equal to find proceeding angles in the same medium, e.g. to find θ3 I imagined a right-angled triangle, where θ2 and θ3 are the other interior angles.
θ3=180-(90+θ2)

I am not sure whether my methodology is correct or appropriate and would appreciate any advice on improvements I could make.

2. I have assumed the same method and proceeded to calculate angles θ2- θ8 accordingly. I must note that I realize the scale of my diagram is too small to properly exhibit the smaller angles (e.g. θ6=3 degrees) and I will draw another larger scale diagram as a better example.

Thank you to anyone who replies

 

[rude man]

Just use Snell's law for all the boundaries. Don't need any 'basic laws of geometry'.
I notice $\theta_3 and \theta_4$ are with respect to the plane rather than to the normal. This is not the way to go.
I can't read your paperwork. Type your text. Use LaTex if you know it or want to learn it.

 

[TSny]

I notice $\theta_3 and \theta_4$ are with respect to the plane rather than to the normal.

The blocks are arranged so that the indicated angles are all with respect to the normals.

 

[TSny]

I am not sure whether my methodology is correct or appropriate and would appreciate any advice on improvements I could make.
...
I must note that I realize the scale of my diagram is too small...

I think your method is correct.

You might see if you can relate $\theta_8$ directly to $\theta_1$ in one equation by combining the separate Snell's law equations before plugging in any numbers. You can then use this one equation to calculate $\theta_8$ for parts 1 and 2. Something interesting occurs regarding $n_C$.

 

[TSny]

I think your method is correct.

You might see if you can relate $\theta_8$ directly to $\theta_1$ in one equation by combining the separate Snell's law equations before plugging in any numbers. You can then use this one equation to calculate $\theta_8$ for parts 1 and 2. Something interesting occurs regarding $n_C$.

The single equation relating $\theta_8$ directly to $\theta_1$ is applicable if there aren't any total internal reflections. So, I guess you still need to find the intermediate angles to identify any total internal reflections. My idea of a single formula might not be such a good idea after all. Edit: Also, the question statement asks you to find all the angles! And, you need all the angles to trace the ray.

Check your work for part 2 at the A-B interface.

 

[hutchphd]

I think your method is correct.

You might see if you can relate $\theta_8$ directly to $\theta_1$ in one equation by combining the separate Snell's law equations before plugging in any numbers. You can then use this one equation to calculate $\theta_8$ for parts 1 and 2. Something interesting occurs regarding $n_C$.

Also if $n_A =n_B$ then the result is very interesting (and correct). I found it easiest to measure all the angles with respect to the vertical axis and use cosines in "Snell's Law" for the $AB$ interface. All you then need is $cos^2+sin^2=1$ The appropriate choice of square root takes care of any possible total internal reflection I think.

 

[rude man]

View attachment 264713

The blocks are arranged so that the indicated angles are all with respect to the normals.

Right you are.