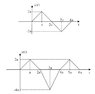
Response of LTI System A to x(t): y(t)=x(t)-x(t-2a)

  • Thread starter Thread starter peripatein
  • Start date Start date
  • Tags Tags
    Convolution
AI Thread Summary
The discussion focuses on determining the response y(t) of LTI system A to the input x(t), expressed as y(t) = x(t) - x(t-2a). The user seeks clarification on how to derive this relationship, particularly for the interval 2a < t < 4a. The equations for x(t) and y(t) are provided, highlighting their behavior in specified time intervals. The user asks for agreement on the derived equations of the lines, indicating a need for validation of their calculations. Understanding the relationship between y(t) and x(t) is crucial for analyzing the system's response.
peripatein
Messages
868
Reaction score
0
Hi,
y(t) is the response of LTI system A to x(t). How could I have figured out that y(t) = x(t) - x(t-2a) (please see attachment). By looking at the graphs this isn't apparent to me :S.
 

Attachments

  • Untitled2.jpg
    Untitled2.jpg
    16.7 KB · Views: 475
Engineering news on Phys.org
Write out the equations of the lines. You know that the equations are equal for 0<t<2a and 4a<t<6a.

Write out the equation of y(t) for 2a<t<4a. Relate that equation to the equation for x(t).
 
x(t) = 2t - 2(t-a) + 2(t-3a) - 2(t-4a)
y(t) = 2t - 2(t-a) - 4(t-2a) + 4(t-3a) + 2(t-4a) - 2(t-5a) + 2(t-6a)
These are the equations of the lines. Would you agree?
 

Thread 'Underwater piezoelectric sensor array receive sensitivity'

Hi all I have some confusion about piezoelectrical sensors combination. If i have three acoustic piezoelectrical sensors (with same receive sensitivity in dB ref V/1uPa) placed at specific distance, these sensors receive acoustic signal from a sound source placed at far field distance (Plane Wave) and from broadside. I receive output of these sensors through individual preamplifiers, add them through hardware like summer circuit adder or in software after digitization and in this way got an...
View full post »

Thread 'Following up on the recent thread about Earth Resistance measurements'

I have recently moved into a new (rather ancient) house and had a few trips of my Residual Current breaker. I dug out my old Socket tester which tell me the three pins are correct. But then the Red warning light tells me my socket(s) fail the loop test. I never had this before but my last house had an overhead supply with no Earth from the company. The tester said "get this checked" and the man said the (high but not ridiculous) earth resistance was acceptable. I stuck a new copper earth...
View full post »

Thread 'Question about bonding ground and neutral'

I am not an electrical engineering student, but a lowly apprentice electrician. I learn both on the job and also take classes for my apprenticeship. I recently wired my first transformer and I understand that the neutral and ground are bonded together in the transformer or in the service. What I don't understand is, if the neutral is a current carrying conductor, which is then bonded to the ground conductor, why does current only flow back to its source and not on the ground path...
View full post »

Similar threads

Why is convolution used to represent LTI output?
Replies
7
Views
3K
Control Theory -- Systems where the controller also changes with time
Replies
1
Views
1K
Question about an LTI System and its Frequency Response
Replies
2
Views
2K
Output as the convolution of the Impulse response and input
Replies
5
Views
4K
Physical/conceptual reason for inductor voltage step response
Replies
4
Views
2K
BIBO Stable if and only if impulse response is summable
Replies
2
Views
5K
Time Invariance of System with x(t) and y(t) Equations
Replies
4
Views
1K
Alternator torque when connected to a phase-shifted AC source
Replies
3
Views
2K
Does every control system contain an integrator?
Replies
10
Views
3K
Convolution Integral properties
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top