Why is convolution used to represent LTI output?

[Nikitin]

Hi. If you have a LTI system with an impulse response function $h(t)$ taking in an input $x(t)$, why does its output $y(t)$ become

?

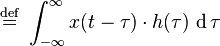
I realize $y(t)$ not only depends on the instantaneous input $x(t)$, but also on the lingering effects of previous inputs $x(\tau)$ with $\tau < t$. But how does the convolution integral model this?

 

[Nikitin]

OK I found a mathematical proof on wikipedia. It is coherent, but gives zero physical insight (is this the norm in EE?).

http://en.wikipedia.org/wiki/LTI_system_theory#Continuous-time_systems

However, why does the input $x(u)$ and output $y(t)$ have different domains there? Is it because the range of $y(t)$ is directly dependent on every element in the range of $x(t)$?

 

[Stephen Tashi]

There are LTI systems that do not need to be represented by a convolution. So I think the best intuitive approach is to ask why the most general LTI system is represented by a convolution and why all apparently simpler LTI systems can be regarded as being implemented by a convolution.

Suppose the rule for a system S(t) is "the output y(t) is 4 times the input x(t)".
The notation for this can be confusing, since S can be regarded as function t, but we are also thinking of it as function of x(t).
So , abusing notation, S(t) = S( x(t) ) = 4 x(t).
This system is linear. S( A g(t) + B r(t)) = A S(g(t)) + B S(r(t)).
The output is shift invariant in the sense that S(t-h) = S(x(t-h)) = S applied to input function evalated at t-h..

A slightly more general system is
S(t) = S( x(t)) ) = 4 x(t) + 3 x(t-1) + 2 x(t+1)
This is also linear and shift invariant.

This suggests a more general form for LTI systems is:
$S(t) = \sum_{i=0}^N A_i x(t-h_i)$ where the $A_i$ and $h_i$ are constants.

If the $h_i$ are all distinct numbers then we can define a function $g(h)$ that maps the value $h_i$ to the coefficient $A_i$

Rewriting the above summation in terms of g():

$S(t) = \sum_{i=0}^N g(h_i) x(t - h_i)$

To further generalize, we replace summation by integration

$S(t) = \int_H g(h) x(t-h) dh$ where $H$ is the range of values that $h$ may take.

 

[Baluncore]

OK I found a mathematical proof on wikipedia. It is coherent, but gives zero physical insight (is this the norm in EE?).

Mathematical solutions are deliberately generalised to avoid physical insight as that makes mathematics universally applicable.

So, without using mathematical symbols, why convolution? The important thing is that, being linear, there is no cross-modulation of the signals in the system. All the different frequencies in the response are therefore amplitude and phase independent of each other. The transfer function is then simply the amplitude and phase response of the system to any sinusoidal stimulation. That is not true, as you suggest in the time domain, where all the stimulations and responses are summed in all of time.

 

[Mike_In_Plano]

I have a more intuitive means of appreciating the power of convolutions.
If you think of the LTI as it responds to a short impulse, you have the impulse function.
If you imagine the input signal as a stream of impulses of various magnitudes, you can imagine the system responding to each impulse.
If you graph the response to the first impulse, then graph the response of the second response under it, and continue making graphs down the page, you'll see that the responses are all the same except for magnitude and a slight delay to account for when each impulse happens.

Now, if you make a "totaled" graph at the bottom by adding the values of each graph (y_total(t) = x1(t) + x2(t) +x3(t)... ) above, you get the cumulative effect of the signal over time.
This is essentially what happens when you perform the integration, but this has always seemed "right" to me as it allows you to better imagine the process behind the math.

 

[Stephen Tashi]

The way I look at it, the contribution to the output that input x() makes is "locally linear". At t -h it adds some constant multiple of x(t-h) to the output at t. So you can think of the net output as a sum of the form g(h)x(t-h) where g(h) is a function that tells you what constant to multiply x(t-h) by. (This probably amounts to the "impulse response" view.) If the contribution of the input at t-h was a nonlinear expression like $(x(t-h))^2$ then the output wouldn't be a linear function of the input.

 

[Nikitin]

OK, thanks guys. I think I get it now!

EDIT: If anybody is wonder about the same thing as me, check out this http://www.quora.com/What-is-an-intuitive-explanation-for-convolution too.

 

[atyy]

The simplest way to think about convolution is that for a system that responds immediately that is linear, we get y(t)=hx(t). If it doesn't respond immediately, we can try y(t) =h(0).x(t) + h(1).x(t-1) + h(2)x(t-2) + ..., which written in summation notation is y(t) = sum {h(n)x(t-n)} which is the convolution.

An explicitly non-convolutional form for an LTI system is dy/dt = -y + x. Here I chose the minus sign so that the system doesn't explode when the input x is zero. I think you can show using the impulse response view (make x a delta function) and linearity for superposition to get the convolutional form out of it. I'm not sure I got everything there correct, but you can google "Green's function" for the thing that translates between the differential and integral forms for LTI systems. Also, here I've only used 1 variable.

http://en.wikipedia.org/wiki/Green's_function
http://en.wikipedia.org/wiki/Impulse_response

When one goes to nonlinear systems, the most "general" "nonexploding" convolutional TI approximator in some sense is Volterra series. This precise conditions of this theorem is given by Boyd and Chua http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.126.9363. The usual convolution is just the linear term of the Volterra series.